対応のあるデータの差を検定する
前回のブログ記事では「対応なしt検定」について見ていきました。
今回は「対応ありt検定」で例題を解いていきましょう。
今回も統計解析ツールjamoviを使ってデータ分析を行っていきます。
お題「2種類の試行の差の確認」
#今回のお題は以下を考えます。
ある組織では静的解析ツールを用いてプログラムのソースコードから欠陥候補を抽出している。
これまで設定Aでツールを運用してきたが、新しく設定Bを作成した。
設定Aと設定Bの2種類の設定で、静的解析ツールの欠陥抽出数に差があるかどうかを確認したい。
設定Bの方が性能が良ければ設定Bを標準としたい。
異なる開発者が作成したソースコードをランダムに7個抽出し、設定Aと設定Bのそれぞれの設定で欠陥候補を抽出した。
データの単位は欠陥候補数とする。
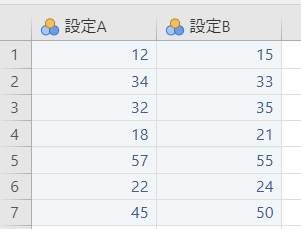
| 設定A | 設定B |
|---|---|
| 12 | 15 |
| 34 | 33 |
| 32 | 35 |
| 18 | 21 |
| 57 | 55 |
| 22 | 24 |
| 45 | 50 |
さっそくjamoviにデータを設定します。
データパネル
記述統計での確認
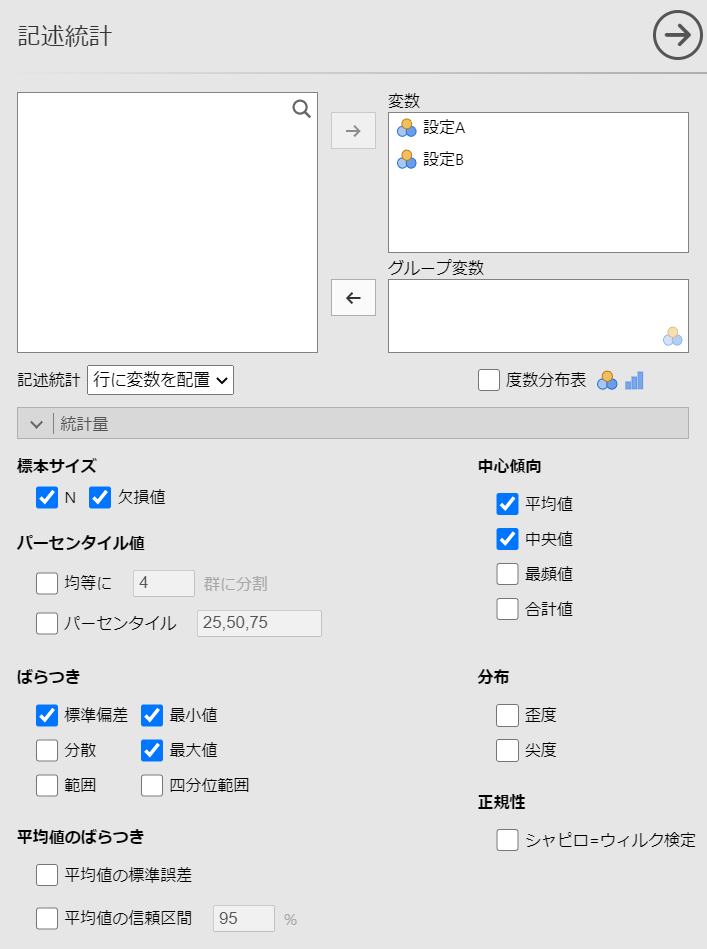
#メニューの「分析」-「探索」-「記述統計」を選択します。
統計量の設定を以下のように行います。
(記述統計「行に変数を配置」を選択しています)
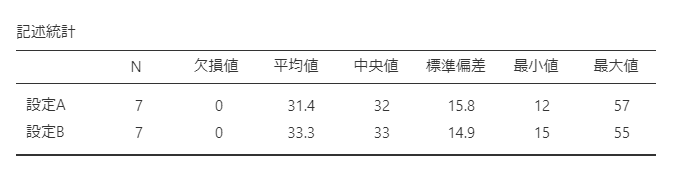
記述統計データが以下のように表示されました。
平均値と中央値の値は、設定Aよりも設定Bの方が大きくなっています。
感覚的にですが「設定Aよりも設定Bの方が欠陥候補の抽出数が大きい」ように見えます。
しかし、得られたデータには設定Bの方が欠陥候補数が少ないケースもあるので判断に迷うところです。
今回は「対応のある2群(ペア)のデータの差を検定する」のでt検定は「対応ありt検定」を選択します。
対応ありt検定での確認
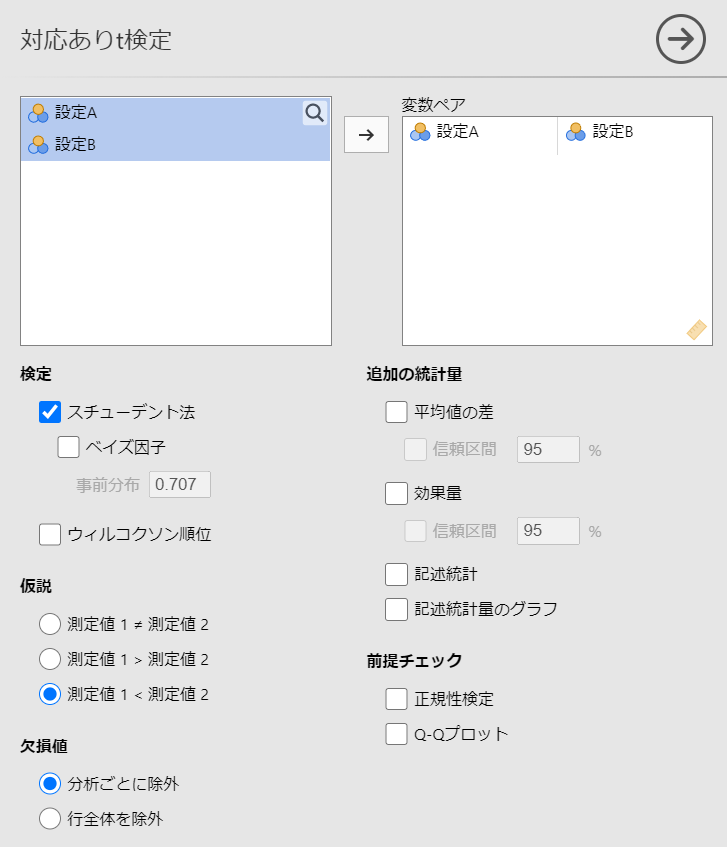
#メニューの「分析」-「t検定」-「対応ありt検定」を選択し、以下のように設定します。
対応ありを選択したので、変数がペアとして横一列に並んでいます。
対立仮説として「設定Aよりも設定Bの方が欠陥候補の抽出数が大きい」にするので、仮説の部分は
測定値1 < 測定値2
としています。
検定結果として以下の値が得られました。
p値は0.047で5%以下なので、帰無仮説は棄却され、
欠陥候補の抽出能力は「設定A < 設定B」と言える、となりました。
まとめ
#同一の被験対象に2つの施策を実施したときに、効果に差があるかどうかが判断できました。
これまでのブログ記事でjamoviが提供する3つのt検定機能
- 対応なしt検定
- 対応ありt検定
- 1標本t検定
を紹介できました。
よろしければ他のブログ記事も参照ください。
データ分析に活用して頂ければ幸いです。