水準が3つ以上のデータを分析したい
これまで「対応あり・なしの2つのデータ群について差」の検定を実施してきました。
では、3つ以上のデータ群の差を検定するにはどうすればいいでしょうか?
実はt検定は2群の差までしか検定することが出来ません。
3つ以上の条件での分析には「分散分析」を用いることになります。
今回も統計解析ツールjamoviを使ってデータ分析を行っていきます。
要因・水準について
#今後必要になるので統計用語について説明しておきます。
統計では「改善前、改善後」などの条件を「水準」と呼びます。
「改善前、改善後」は条件が2つですから、水準は「2」となります。
水準とはあまり馴染みのない言葉だと思いますが、水準は「要因を質的・量的に変更させた”条件”」のことです。
また、要因とは「実験結果に影響を与える原因」のことを言います。因子とも言います。
お題「水準が3つ以上のデータを分析せよ」
#今回のお題は以下を考えます。
ある組織でソフトウェア品質改善活動を実施してきた。
これまで品質改善活動の完了条件を条件Aや条件Bとしてきたが、今回は条件Cを新しく追加した。
品質改善活動後に実施したソフトウェアモジュールの結合試験における欠陥密度において有意な差があるかを確認したい。
結合試験結果は以下のサンプルデータを用いて検定する。(一回の品質改善活動で適用する条件は一つのみとする)
データの単位は欠陥件数/KLocとする。
| 条件A | 条件B | 条件C |
|---|---|---|
| 2.4 | 2.5 | 2.6 |
| 2.7 | 2.6 | 2.5 |
| 2.6 | 2.4 | 2.4 |
| 2.7 | 2.7 | 2.6 |
| 2.9 | 2.5 | 2.4 |
| 2.5 | 2.6 | 2.5 |
| 2.9 | 2.4 | 2.4 |
| - | 2.3 | 2.3 |
| - | - | 2.5 |
さっそくjamoviにデータを設定します。
データパネル
要因:品質改善活動の完了条件(1要因)
水準:条件A、条件B、条件C(3水準)
対応なしt検定での結果
#同一モソフトウェアジュールに複数の条件を適用しないとしたので、結合試験結果はそれぞれ独立していると考えます。
ちょっと考えると「対応なしt検定」が適用できそうに思いますが、水準が3つ以上なので「対応なしt検定」を適用しようとしてもjamoviに怒られてしまいます。
記述統計での確認
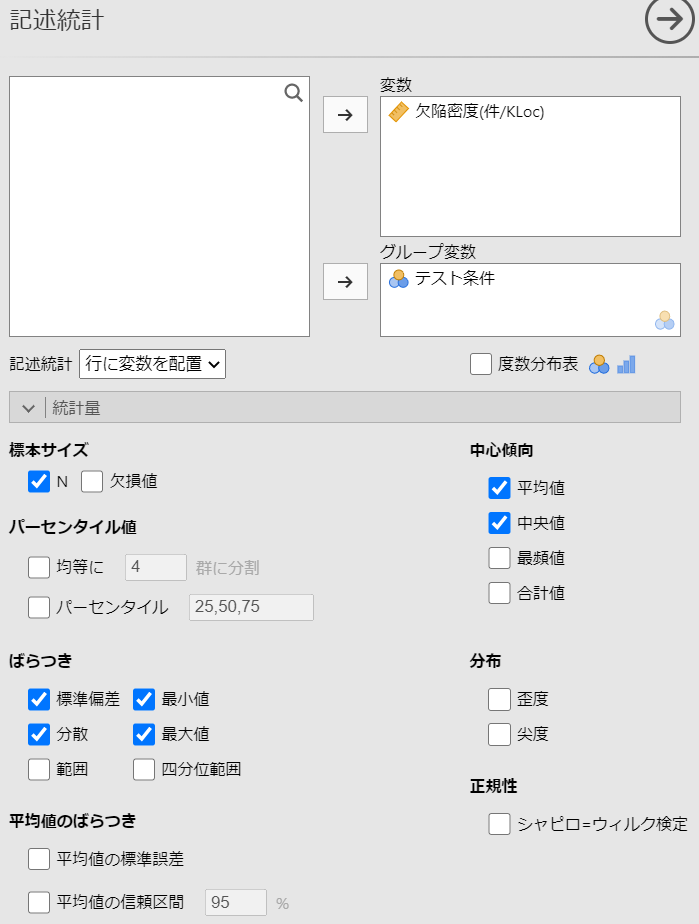
#メニューの「分析」-「探索」-「記述統計」を選択します。
統計量の設定を以下のように行います。
(記述統計「行に変数を配置」を選択しています)
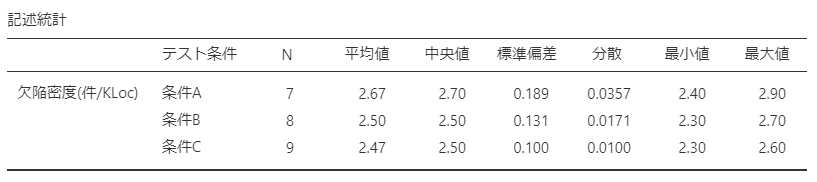
記述統計データが以下のように表示されました。
平均値と中央値の値は、条件Aよりも条件Bや条件Cの方が小さくなっています。
感覚的にですが「条件Aと条件B・条件Cの間には差がありそう」ですが「条件Bと条件Cの間には差はなさそう」に思います。
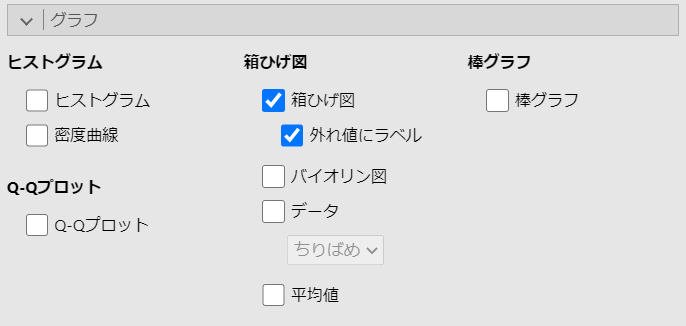
箱ひげ図でも確認してみましょう。
以下の設定をします。
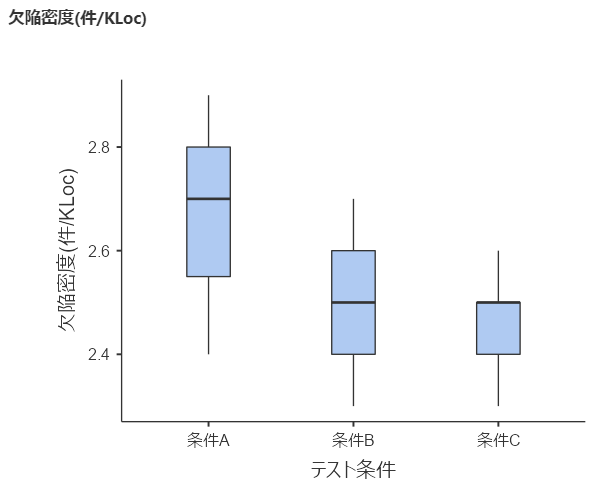
箱ひげ図が以下のように表示されます。
外れ値は確認できません。
目視なのでかなりアバウトな判断になりますが
条件A > 条件B ≒ 条件C
のように見えます。
今回は「1要因(因子)における対応のない3群(水準)のデータの差を検定する」ので「1要因分散分析」を選択ます。
1要因分散分析での確認
#メニューの「分析」-「分散分析」-「1要因分散分析」を選択し、以下のように設定します。
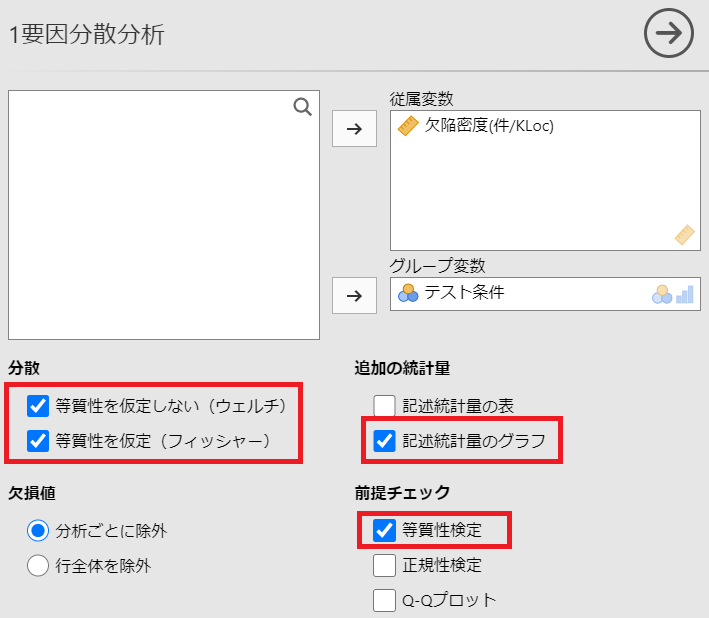
分散の項目は
等質性を仮定しない(ウェルチ)
等質性を仮定(フィッシャー)
の両方をチェックします。
また「記述統計量のグラフ」、「等質性検定」にもチェックを入れます。
検定結果として以下の値が得られました。
これは困りました。
ウェルチ法とフィッシャー法でp値の値がかなり異なります。
ウェルチ法では「有意差なし」、フィッシャー法では「有意差あり」となってしまいます。
ウェルチ法では分散の等質性を仮定していないのですが、実際に等質性を検定する必要がありそうです。
そこで先ほどチェックした「等質性検定」のデータを確認します。
前提チェックというデータが確認できます。
分散等質性検定(ルビーン検定)の結果、p値は0.25なので「分散の等質性に差はない」という帰無仮説を棄却できないので「分散の等質性は”あり”」と考えます。
よって、先ほどの検定手法のうち「フィッシャー法」(等質性を仮定)の方の値(p値:0.022)を採用したいと思います。
結果として「データに有意差はあり」と考えます。
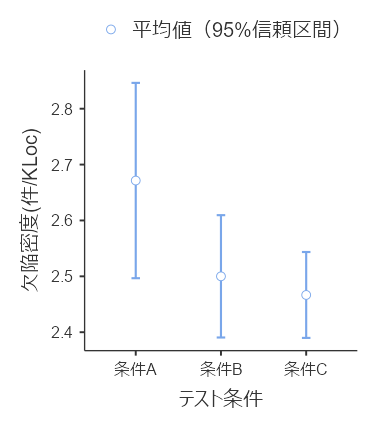
念のため、グラフも確認しておきましょう。
水準間での影響の差
#有意差があることはわかったのですが、どの条件間に差があるのかはまだ分かりません。
見た目では
条件A > 条件B ≒ 条件C
なんだろうと推測はできますが、ちゃんと数値で示したいと思います。
jamoviは事後検定を行う機能を持っています。
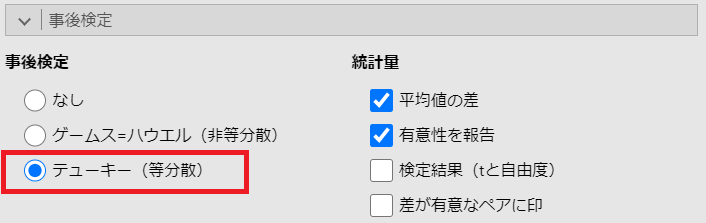
以下のように「事後検定」を設定します。
分散の設定で「フィッシャー法(等質性を仮定)」を選択したので、事後検定では「テューキー(等分散)」を選択しています。
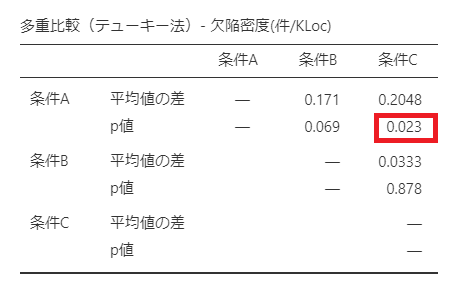
事後分析結果は以下のようになりました。
上表で見る限り、明確に「有意差あり」と判断できるのは
条件A と 条件C の関係
の関係のみだと分かります。
視覚的には差がありそうだった「条件A ― 条件B」の差は有意ではないとなりました。
まとめ
#このように3水準以上の複数水準間での差の検定を実施することができました。
研究室内での実験とは違い、ソフトウェア開発現場で分散分析が当てはまるケースはそれほど多くはないかもしれませんが、複数の条件で開発・試験を実施しているときに、結果に差があるのか無いのかを判断する材料にはなると思います。
よろしければ他のブログ記事も参照ください。
データ分析に活用して頂ければ幸いです。