何となくは通用しない(カイ2乗適合度検定)
取り得る状態が「はい・いいえ」など2つのみのデータの検定(2項検定)を以前のブログで扱いましたが、今回は「多値」データの検定についてご紹介します。
カイ2乗検定とは
#取り得る状態が「はい・いいえ」など2つのみの場合は「2項検定」を使用しましたが、状態が3つ以上の「多値」データである場合の検定は「カイ2乗検定」を使用します。
t検定がt分布を利用した検定であったように、カイ2乗検定もカイ2乗分布を利用した検定です。
t分布は”平均”を扱いますが、カイ2乗分布は”分散”を扱います。
守備範囲が違います。
また、カイ2乗検定には「独立性のカイ2乗検定」と「適合度のカイ2乗検定」があります。
「独立性のカイ2乗検定」は、2つの変数の間に関連があるかを検定します。
「適合度のカイ2乗検定」は、変数の期待度数と観測度数の一致具合を検定します。
今回は以下の例題を通して、期待度数に対して実際の観測度数の一致具合を「適合度のカイ2乗検定」で確認してみましょう。
例題「フロントローディングを証明せよ」
#あるソフトウェア開発組織では、開発工程で検出される欠陥がどの工程で作り込まれた物かを調べるために「欠陥作り込み工程」のメトリクスを収集していた。
この組織では「フロントローディング開発」を目指しており、仕様、設計、実装の各工程で検出される欠陥の比率を以下になるように定めていた。
| 仕様 | 設計 | 実装 | |
|---|---|---|---|
| 欠陥数(%) | 50% | 30% | 20% |
欠陥の作り込み工程が上記の比率から逸脱している場合、プロジェクトを試験工程に移行させることが出来ない。
品質保証部からは「設計・実装で多くの障害が発見されているのに仕様工程での欠陥検出数が少ないのは何か問題があるはずだ」と釘を刺されている。
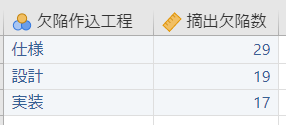
あるプロジェクトから次のようなデータが提出された。
| 仕様 | 設計 | 実装 | |
|---|---|---|---|
| 欠陥数(件) | 29 | 19 | 17 |
その時の品質保証部と開発部との会話は以下のようであった。
品証:「設計・実装工程で検出された欠陥件数が仕様工程で検出された欠陥件数を大幅に上回っている。これでは次工程への移行を許可できない」
開発:「仕様工程では29件、設計・実装工程では合計36件。その差は7件しかないですが…」
品証:「7件も多い!7件は仕様工程の欠陥件数の約25%。設計・実装工程での欠陥件数の約20%にあたる。数字で納得させてもらいたい」
数値を出されてしまった開発部員はどうやって品質保証部員を納得させれば良いだろうか?
「何となく今回は大丈夫」や「自分に免じて」という理由は通用しない。
目標とどの程度かけ離れているかを検定で確かめることにした。
カイ2乗適合度検定
#メニューから「分析」-「度数分析」-「多値目的変数(カイ2乗適合度検定)」を選択します。
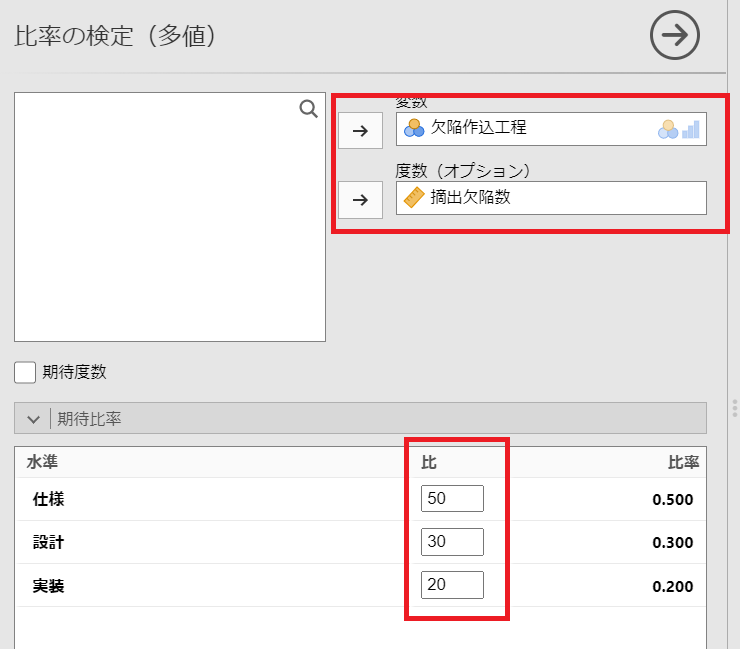
設定パネルが表示されるので、以下のように設定します。
「期待比率」には
仕様:50
設計:30
実装:20
を設定します。
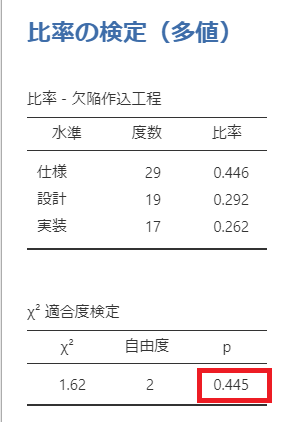
すると以下のような結果が得られました。
p値の扱いはこれまでと同じです。
帰無仮説、対立仮説が
帰無仮説:観測度数と期待度数の分布は一致する
対立仮説:観測度数と期待度数の分布は一致しない
なので、今回は「p値=0.445」のため、帰無仮説が棄却できず
観測度数と期待度数の分布は一致する
となります。
目標として定めた比率から逸脱していないと結論を出しました。
数値を使って品質保証部に説明が出来る状態になりました。
まとめ
#扱うデータの種類によって正規分布、t分布、カイ2乗分布、F分布などを使い分ける必要がありますが、パターンが分かってしまえば個々に対応した検定方法は確率されていますから、jamoviは強力な分析ツールになってくれます。
身近にあるデータをサッと分析して、判断に役立てることが出来ます。
データ分析に活用して頂ければ幸いです。