ベイズ推定を学ぶ ~2項推定~
さまざまな分野でベイズ統計が活用されています。
筆者はこれまで古典的統計(伝統的な頻度論的統計)をメインで使ってきましたが、最近になってベイズ統計の面白さに惹かれています。
人間の思考に素直に従っているところがベイズ統計の魅力ではないかと考えています。
古典的統計では、本来証明したい仮説を”対立仮説”に置き、対立仮説の「当て馬」として”帰無仮説”を設定します。
そして帰無仮説を「棄却する・棄却しない」をp値というものを使って判定し、
帰無仮説を棄却する → 対立仮説を支持する
帰無仮説を棄却しない → 対立仮説を支持しない
とします。
p値の棄却域は一般的に5%を使用し、この棄却域より大きいか小さいかで判断することになります。
しかし、p値で判断できるのは「帰無仮説が正しいとした場合に母集団から標本が得られる確率」であって、母集団が対立仮説に従う確率ではありません。
帰無仮説は”あわて者の誤り”を防止するためにしっかり確認しますが、”ぼんやり者の誤り”については普段はあまり考察しません。
p値至上主義と言っても良いでしょう。
(100%から”ぼんやり者の誤り”の確率を引いた値を「検定力」と言いますが、その話はまた別の機会に)
棄却域を5%と決めた場合、p値が6%でも帰無仮説が棄却され対立仮説が支持されてしまいます。
5%と6%の間に垂直の壁が立ちはだかっているようです。
ベイズ推定では「確率」を「確率分布」として対象をモデル化し、確率分布をグラフを使って視覚的に表現することで、”確からしさ”をモデル全体で把握することが可能になります。
「ベイズ推定」とは
#ベイズ推定とはベイズの定理を用いた推定手法の一つです。
ベイズの定理の式は
=
ですが、この確率の部分を確率分布(関数)に置き換えます。
確率分布とは「ある事象の取り得るすべての確率を出力する関数」です。
ベイズ推定では事前確率や事後確率、尤度を以下のような”確率分布の関数”とします。
=
ここで
は「事後確率分布」
は「事前確率分布」
です。
また、
は「尤度関数」
は「周辺尤度関数」
です。
上記のは”関数”となっていますが計算すると定数になります。
よってベイズ推定の式は
とみなせます。
つまり「事後確率分布は事前確率分布に尤度関数をかけることで導出できる」と解釈できます。
(は「比例記号(proportionality symbol)」です)
事前確率分布が尤度関数を受けてどのような事後確率分布になっていくかを2項分布(コイン投げのような2値しか取らない確率分布)を使って見てみましょう。
「2項分布」とは
#いきなりベイズ推定を実施する前に「2項分布」について見ておきましょう。
コインの表・裏や、カードの表・裏のように”発生する結果が2種類しか存在しない”試行を「ベルヌーイ試行」と言います。
そしてそのベルヌーイ試行を各々独立に回繰り返した場合において、起こりうる事象のうちの一方の発生確率が回発生する確率を表す分布を「2項分布」と言います。
つまり2項分布はベルヌーイの分布を一般化したものと言えます。
式としては
のように書けます。
具体的にどんな分布なのかをグラフで確認しましょう。
以前紹介したJASPを使って確率分布グラフを作成します。
JASPが提供する検定・推定手法の多くはベイズ統計に対応しており、お手軽にベイズ統計を試すにはうってつけのツールです。
2項分布を確認するのにJASPの「分布」モジュールを利用します。
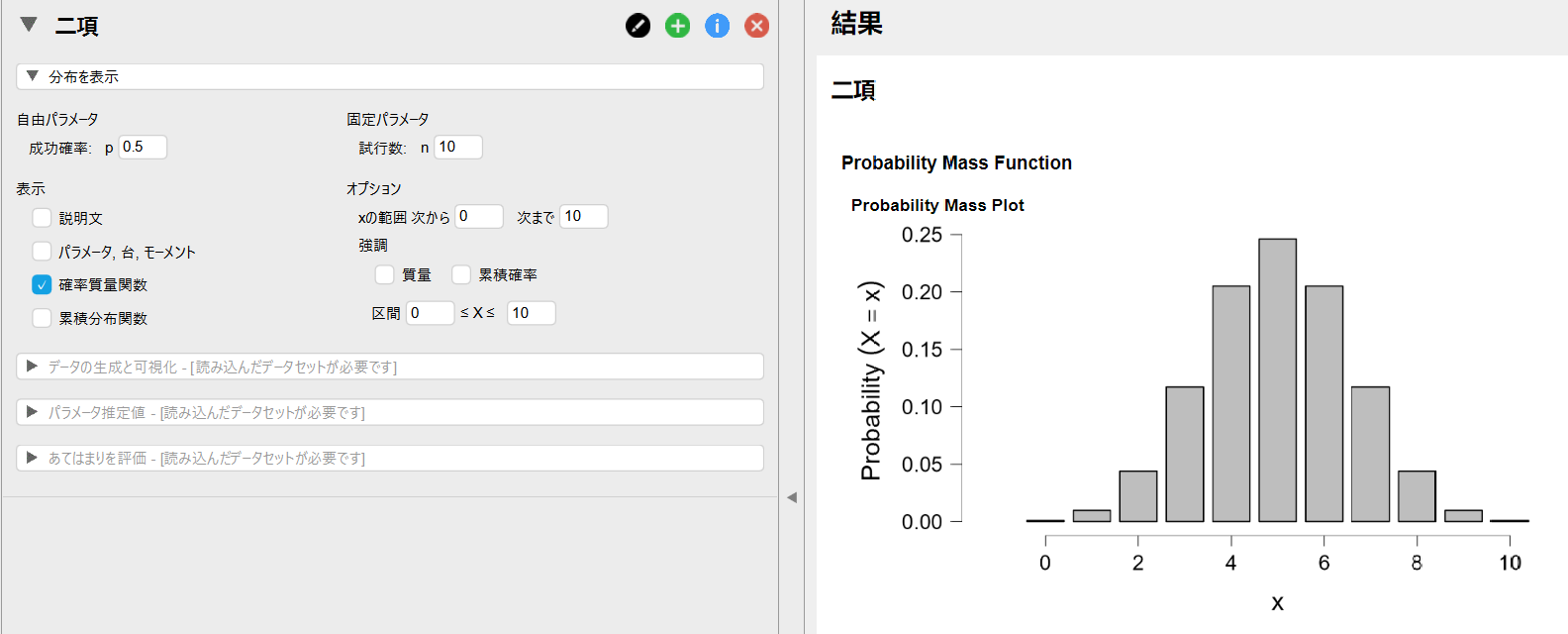
メニューバーに追加された「分布」メニューから「分布」-「離散」-「二項」を選択します。
以下のようなグラフが表示されました。
2項分布は離散分布なので飛び飛びの値を取ります。
試行数や成功確率を変更すると自動的に確率分布が再計算されてグラフが再描画されます。
上記の例では成功確率を0.5に設定しているので、10回試行した場合にもっとも多く発生する成功回数は5回となっています。
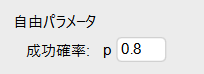
成功確率を0.8に変更してみましょう。
グラフが以下のように更新されました。
グラフの頂点が回数8に移動し、グラフの形がかなり右に偏っています。
上記のグラフを見ると確率0.5はほぼ発生しないと言ってもいいでしょう。
このようにグラフにすると視覚的に状況を把握しやすくなります。
「2項推定」でベイズ推定を学ぶ
#ベイズ推定を2項推定を用いて実践してみましょう。
JASPの「ベイズを学ぶ」モジュールを利用します。
メニューバーに追加された「ベイズを学ぶ」メニューから「カウント」-「二項推定」を選択します。
以下のような設定パネルが表示されました。
準備が整ったのでベイズによる2項推定を考えてみましょう。
コインの表の出る確率分布を導出する
#ここに1枚のコインがあり、コイン投げを10回試行した結果
表:8回
裏:2回
が出たとしましょう。
我々が一般的に持っている常識としては「正しいコインの表・裏が出る確率はそれぞれ0.5」のはずです。
(コイン表面・裏面の刻印等の形によっては微妙に差があるかもしれませんが、ここでは無視します)
10回の試行の”実施前”と”実施後”では、コインの”表が出ると予想する確率分布”にどのような変化があるかを考えます。
パラメータを設定していきます。
「カウントデータ」に
成功数:8
失敗数:2
を設定します。
(ツール上ではコイン投げの結果を「表=成功」「裏=失敗」と関連付けて設定します)
「モデル」には緑色の「十字」ボタンを押して「モデル1」を追加します。
分布はデフォルトで「ベータ」が設定されているのでそのままとします。
「事前分布」「事後分布」の設定はそれぞれ「個別」を選択し、すべてチェックを入れます。
推定結果
#以下のような結果が表示されました。
モデル1の行を見ていきます。
「Prior(θ)」は事前分布です。値はベータ分布beta(1,1)となっています。
「Prior Mean」は事前分布の平均値(期待値)です。値は0.5となっています。
「Posterior(θ)」は事後分布です。値はベータ分布beta(9,3)となっています。
「Posterior Mean」は事後分布の平均値(期待値)です。値は0.75となっています。
なぜ事前分布に「ベータ分布」を設定したのでしょうか。
理由は”事前分布と事後分布の確率分布の種類”が同じになるからです。
事後分布(ベータ分布) ← 事前分布(ベータ分布) × 尤度
ベイズ推定ではこのように事前分布と事後分布の確率分布の形を同じになるように置くことが多いです。
分布の形が同じなので得られた出力を次の推定への入力に設定しやすくなります。
利用できる分布の形は他にもいくつかありますが、ここでの説明は割愛します。
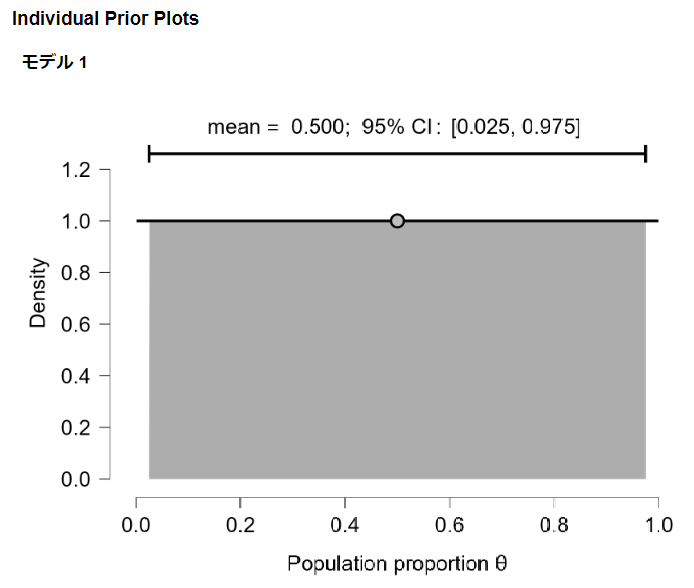
事前確率分布を見てみましょう。
Density(確率密度)がすべて1の”一様分布”になっています。
ベイズでは事前分布に一様分布が良く使われます。
「事前の情報が何もない(事前に知識が何も無い)」場合にはどの確率も一様に等しく発生すると考えられるからです。
次に事後分布を見てみましょう。
大きく右側に偏ったグラフになりました。
コインの試行結果を受けて
このコインはかなり表が出やすい
と推定したことになります。
95%信頼区間を見ると、0.5(正しく作られたコインであれば一番発生しやすい確率)はほとんど左端の淵になっています。
出力結果を事前分布に設定
#先ほど得られた事後分布(beta(9,3))を事前分布に設定して、同じ試行結果を得た時の事後分布の変化を見てみましょう。
以下のように設定を追加・変更します。
「モデル」に「モデル2」を追加し、
α:9
β:3
とします。
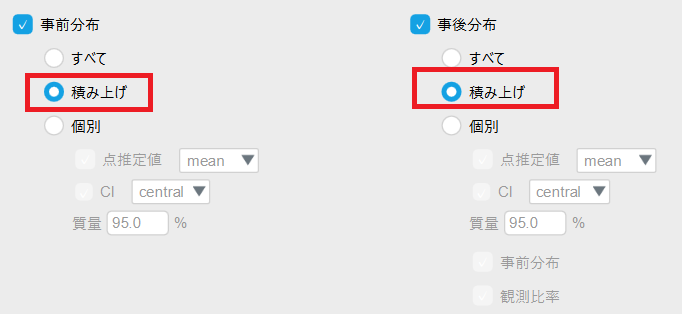
事前分布、事後分布は以下のように「積み上げ」に変更します。
推定結果は以下のようになりました。
モデル2の行を見ると、事後分布はbeta(17,5)となっています。
平均値(期待値)も0.773となり値がさらに1に近づきました。
事後分布グラフを見てみましょう。
確率分布の変化が視覚的に確認できます。
このようにモデル1に比べてモデル2の方がさらに右側に歪んだグラフになっていることが分かると思います。
このように「積み上げ」を設定するとグラフがどのように変化していくのかを確認することが出来ます。
データ数を10倍にしてみる
#先ほどはモデル1の事後分布をモデル2の事前分布に設定しましたが、最初からデータ数が10倍だった場合はどうでしょうか。
モデル2を削除し、モデル1(事前分布 beta(1,1))において
成功数:80
失敗数:20
で確認してみます。
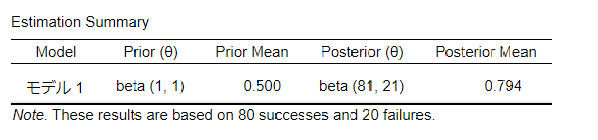
推定結果は以下のようになりました。
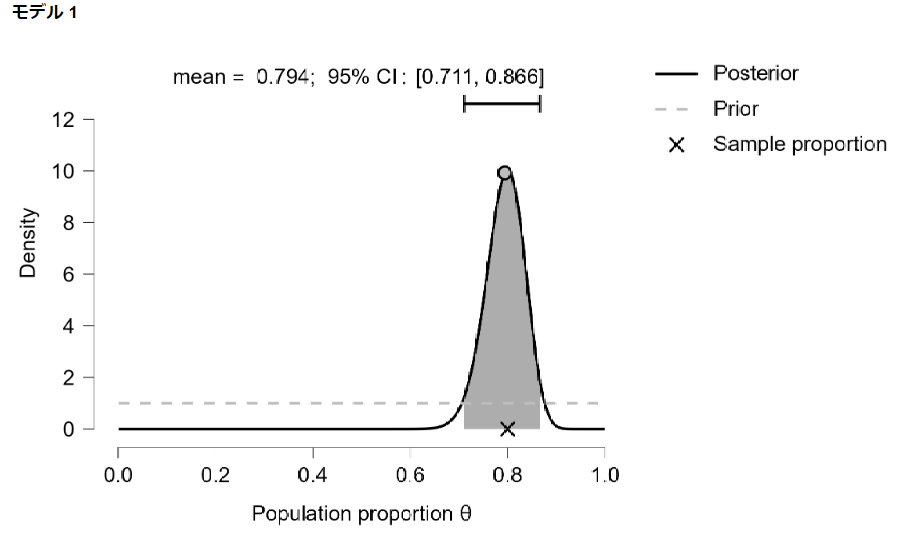
事後分布の平均値(期待値)は0.794になりました。
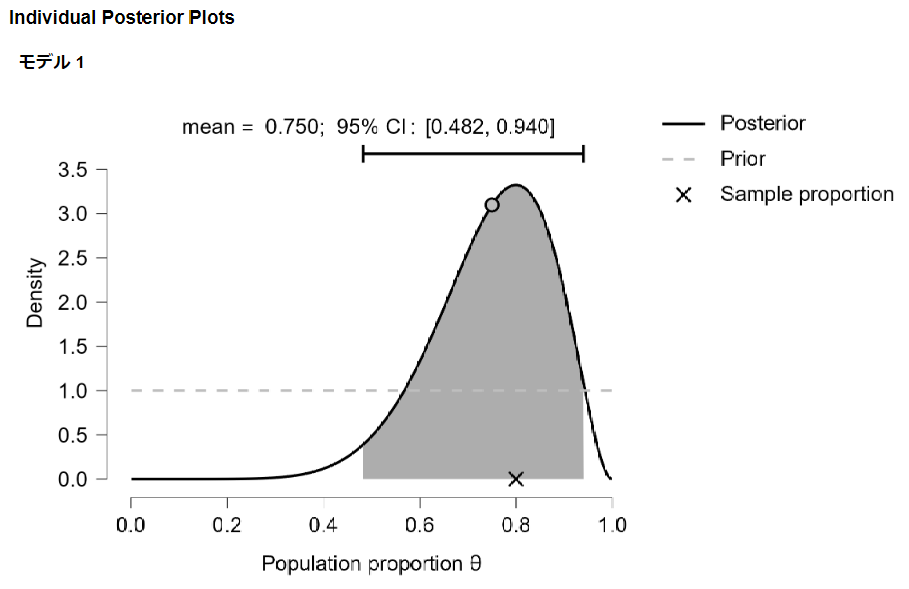
グラフも確認します。
グラフを見ると信頼区間の幅がかなり狭くなり、中央値(最頻値)と平均値(期待値)がほぼ同じと見ていいくらいになっています。
事前分布が誤っていた場合
#次は事前分布(事前に持っていた情報)が”誤っていた”場合を考えてみます。
モデル1の事前分布を beta(1,3) として
成功数:8
失敗数:2
で確認してみます。
推定結果は以下のようになりました。
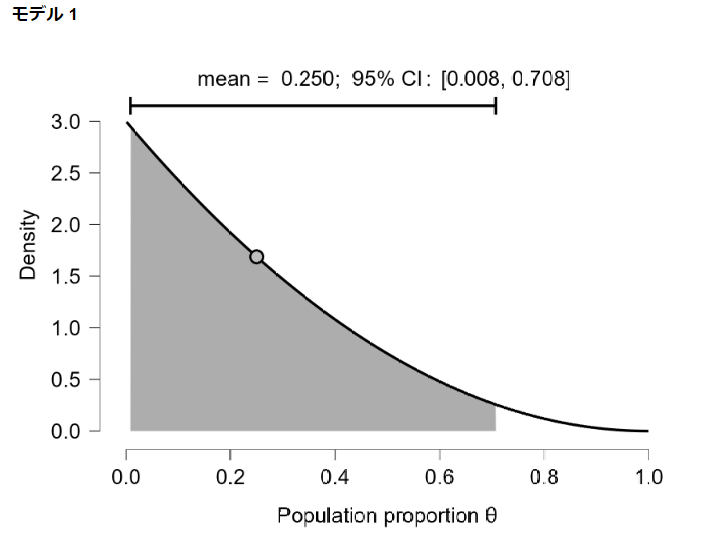
事前分布の平均値(期待値)は0.25であり、事後分布の平均値(期待値)は0.643となりました。
グラフでも確認してみます。
事前分布は以下のようになっています。
beta(1,3)なので、成功よりも失敗の方が確率が高くなっています。
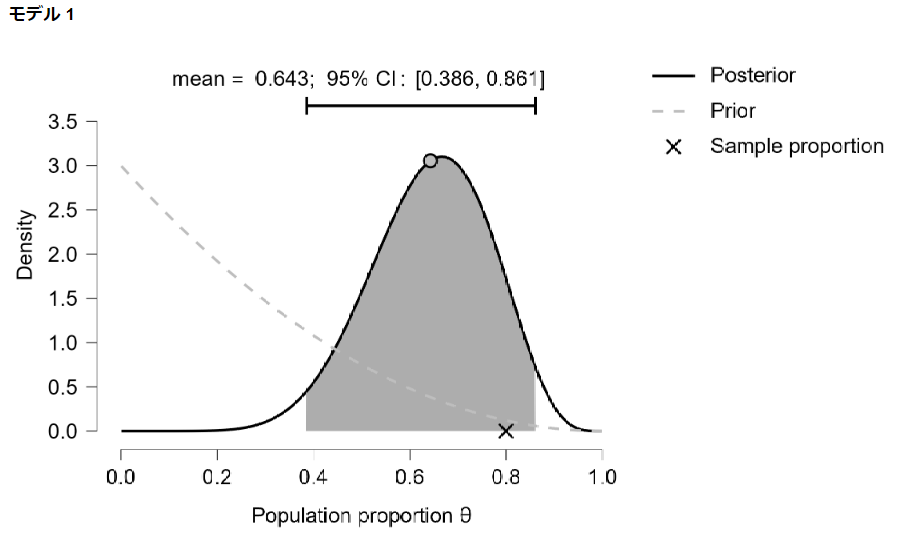
事後分布のグラフは以下のようになりました。
事前情報の影響を受けているため、何も情報を得ていない場合よりも平均値は低い結果となりました。
データ量で事前分布の情報を上書きする
#事前に得ていた情報が誤っていたとしても、データ数が10倍の場合はどうでしょうか。
モデル1の事前分布を beta(1,3) としたままで
成功数:80
失敗数:20
で確認してみます。
推定結果は以下のようになりました。
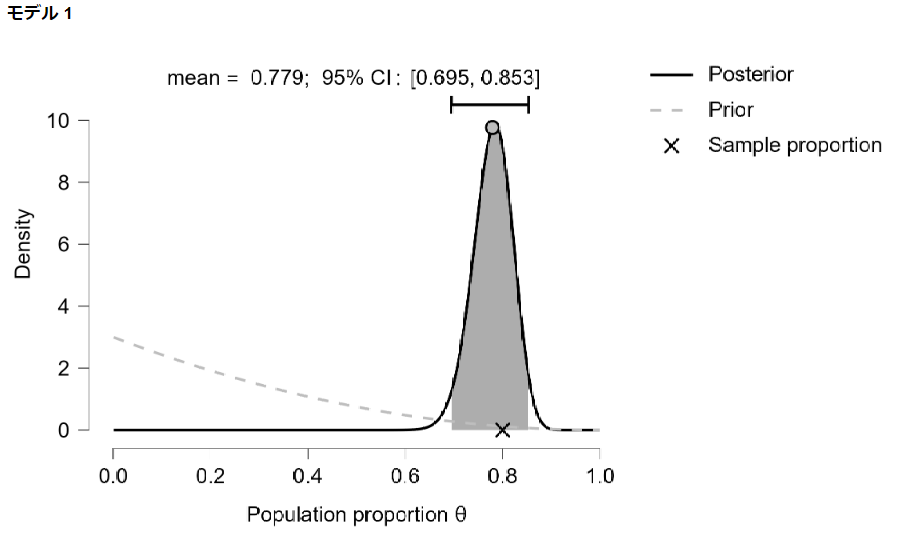
事後分布の平均値(期待値)は0.779となりました。
データ数が10倍になったことで事前分布の影響をほぼ排除できていることがわかります。
事後分布のグラフは以下のようになりました。
まとめ
#以前のブログで”ベイズ更新”を検証しましたが、ベイズ推定では確率を確率分布と捉えて、確率分布が変化していく様子をグラフを使って視覚的に確認することが出来ました。
また事前分布が誤っていた場合でも、入力するデータが多ければ事前分布の形は事後分布にほとんど影響を与えないことを確認することが出来ました。
ベイズ推定を使ってさまざまな意思決定に役立てていただければと思います。
データ分析に活用して頂ければ幸いです。