箱ひげ図と散布図を同時に描画して概要を把握する(描画編)
以前のブログでは「箱ひげ図」を使ったデータの可視化手法をご紹介しました。
今回は「箱ひげ図」と「散布図」を使ってデータの可視化を行っていきたいと思います。
箱ひげ図とは(おさらい)
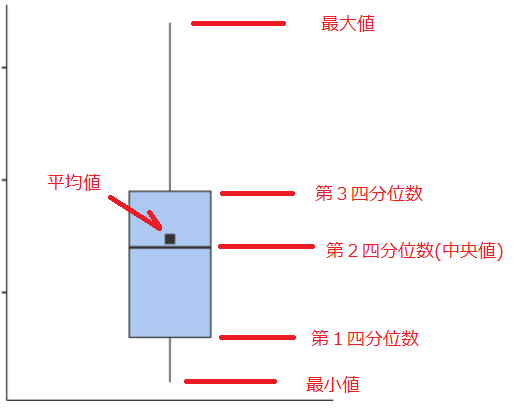
#箱ひげ図とは、下図に示すように最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値を持ち、第1四分位数から第3四分位数までの範囲を箱で描画し、最小値、最大値は箱の両端からそれぞれ線を引き出した図です。
箱は第2四分位数(中央値)で区切ってあります。
下図には平均値を箱の中の黒点で示しています。
箱ひげ図の特徴は
- 最小値から中央値までの間に全データのうちの下側50%のデータが入る
- 中央値から最大値までの間に全データのうちの上側50%のデータが入る
- 箱の中に中央値を中心にして全データのうちの上下50%のデータが入る
です。
箱の形とひげ(線)の長さを見れば、データがどのように散らばっているかについて、おおよその見当がつきます。
また、箱ひげ図によく用いられるルールとして、第1四分位数から第3四分位数の距離(つまり箱の長さ)の1.5倍以上箱から離れた値は”外れ値”として別途描画し、外れ値を除外したデータで箱ひげ図を描画します。
散布図とは
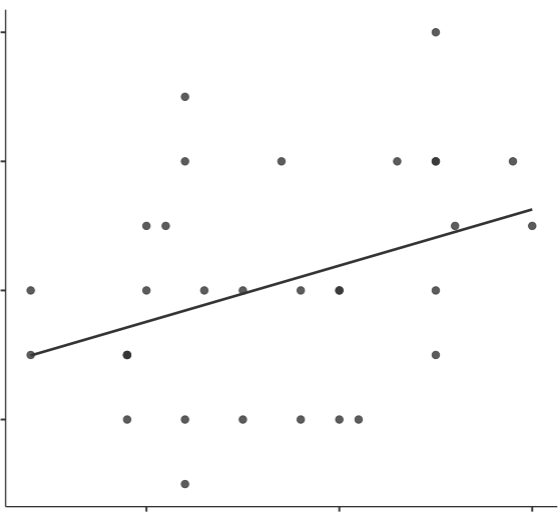
#散布図は、関係のある2項目のデータを縦軸、横軸に点でプロットしたものです。
分布図とも言います。
散布図は相関関係を大まかに把握するときにも使用します。
データ群が右上がりに分布する傾向であれば正の相関があり、右下がりに分布する傾向であれば負の相関があると見ることができます。
上図ではデータが正の相関なのか負の相関なのかが見た目で判断しづらいので、データの回帰直線(線形回帰)を追記してあります。
例題:仕様書レビュー品質状況の把握
#あるソフトウェア開発組織では、仕様書レビューのメトリクスデータを収集しています。
仕様書レビューのメトリクスデータ項目は以下になります。
- レビュー工数密度(人時/頁)
- レビュー指摘密度(件/頁)
レビュー工数密度は1ページあたりにかけるレビュー工数です。
工数の単位は人時(1人が1時間作業する)です。
人時なので、1つの仕様書を3人で2時間レビューした場合は 3 × 2 で6人時のレビュー工数となります。
レビュー指摘密度は1ページあたりに指摘された指摘の数です。
今回は簡単化のため、指摘の重み(重要度)は考慮せずに指摘1件として処理します。
個々の成果物の品質状況にムラがあると考えた品質保証部は、仕様書レビュー結果をもとにして何らかの対策を打ちたいと考えています。
品質保証部長の指示を受けた品質保証部員は仕様書レビューのメトリクスデータを開発部門から取り寄せました。
まずはデータの可視化から始めることにしました。
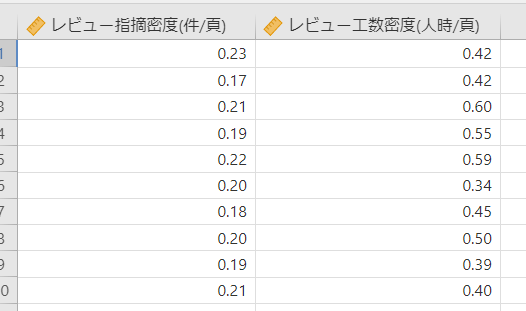
仕様書レビューのメトリクスデータの詳細は以下です。
総件数:32件
| レビュー指摘密度(件/頁) | レビュー工数密度(人時/頁) |
|---|---|
| 0.23 | 0.42 |
| 0.17 | 0.42 |
| 0.21 | 0.6 |
| 0.19 | 0.55 |
| 0.22 | 0.59 |
| 0.2 | 0.34 |
| 0.18 | 0.45 |
| 0.2 | 0.5 |
| 0.19 | 0.39 |
| 0.21 | 0.4 |
| 0.2 | 0.43 |
| 0.18 | 0.42 |
| 0.28 | 0.5 |
| 0.24 | 0.55 |
| 0.22 | 0.55 |
| 0.19 | 0.39 |
| 0.22 | 0.42 |
| 0.18 | 0.39 |
| 0.22 | 0.53 |
| 0.18 | 0.51 |
| 0.2 | 0.55 |
| 0.19 | 0.39 |
| 0.2 | 0.45 |
| 0.18 | 0.48 |
| 0.21 | 0.41 |
| 0.2 | 0.4 |
| 0.19 | 0.34 |
| 0.2 | 0.48 |
| 0.18 | 0.5 |
| 0.22 | 0.55 |
| 0.21 | 0.56 |
| 0.22 | 0.47 |
上表のデータを統計解析ツールjamoviに設定します。
記述統計量
#まず最初に記述統計量を計算してみましょう。
jamoviでは簡単に記述統計量を算出することができます。
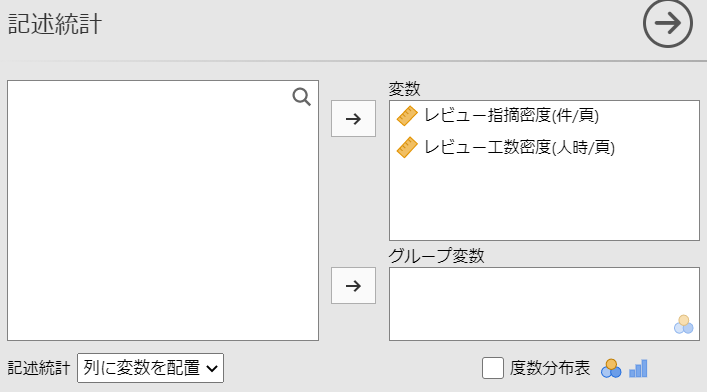
「メニュー」―「探索」―「記述統計」を選択します。
設定パネルを以下のように設定します。
記述統計量が以下のように出力されました。
基本的な統計量である平均値や中央値、標準偏差などがわかります。
箱ひげ図
#データを可視化していきます。
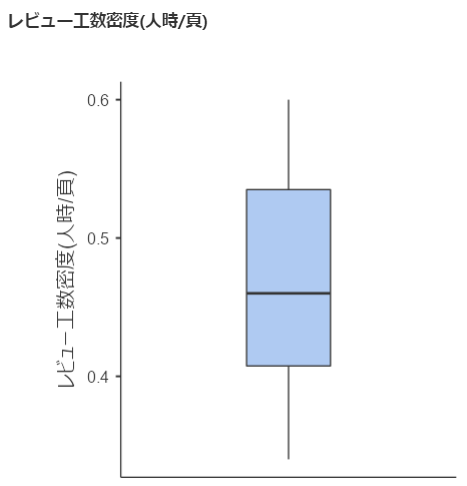
箱ひげ図を単独で描画してみましょう。
設定パネルの「グラフ」の部分を以下のように設定します。
レビュー指摘密度(件/頁)とレビュー工数密度(人時/頁)について箱ひげ図を描画することが出来ました。
上記の2つの箱ひげ図を見ると、レビュー指摘密度の方はデータNo.13が外れ値になっていることがわかります。
このNo.13に相当する成果物(仕様書)のレビューでは、何か問題が発生している可能性があります。
取り急ぎ、情報を記録しておきます。
個々の「箱ひげ図」を単独で確認することでも、ある程度の品質傾向はわかります。
しかしせっかく対応のあるデータなので、両方のデータを散布図にして確認してみます。
そして、散布図に箱ひげ図も加えて描画してみましょう。
散布図の軸にそれぞれ箱ひげ図を当てはめる
#「メニュー」―「探索」―「散布図」を選択します。
設定パネルの「散布図」の部分を以下のように設定します。
今回は回帰直線・曲線に「直線」、グラフ周辺部に「箱ひげ図」を選択しています。
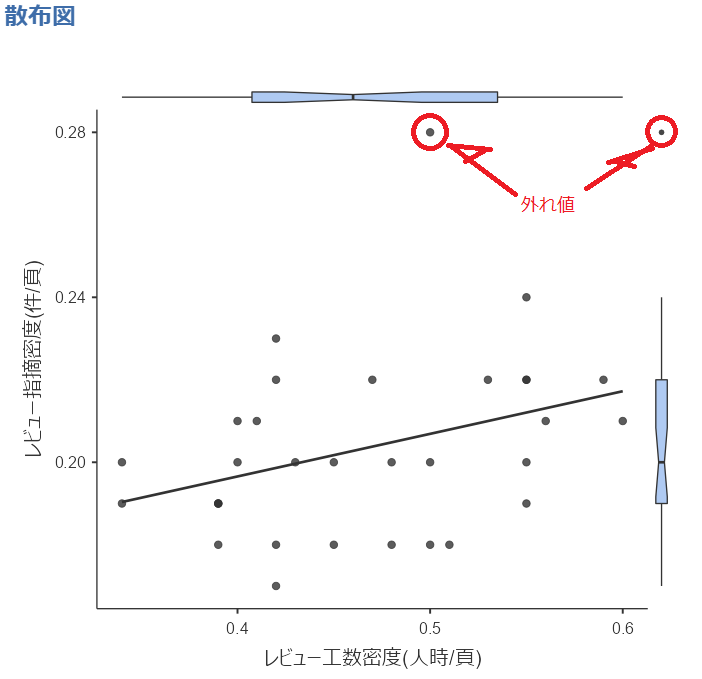
以下のような散布図が描画されました。
グラフの横軸と縦軸に対応した「箱ひげ図」も一緒に描画されています。
jamoviの散布図に付属する箱ひげ図は中央値のあたりが「くびれた」形になっています。(どうしてそのようにしたのか理由はわかりませんが)
散布図を見ると、図の上部に先ほど確認した「外れ値(No.13)」が見えます。
右端に描画されている箱ひげ図でも「外れ値」であることがわかります。
このように散布図に箱ひげ図を一緒に描画することによって、簡単に外れ値を見つけることが出来ます。
外れ値を含んだままデータを可視化すると外れ値にグラフが引っ張られてしまうので、以前のブログ"箱ひげ図で外れ値を確認する"で実施したように、外れ値を除外して再度描画してみましょう。
ただし、外れ値データを持つ仕様書(レビュー結果)については、別途検討が必要です。
「除外する」=「検討しない」というわけではありません。
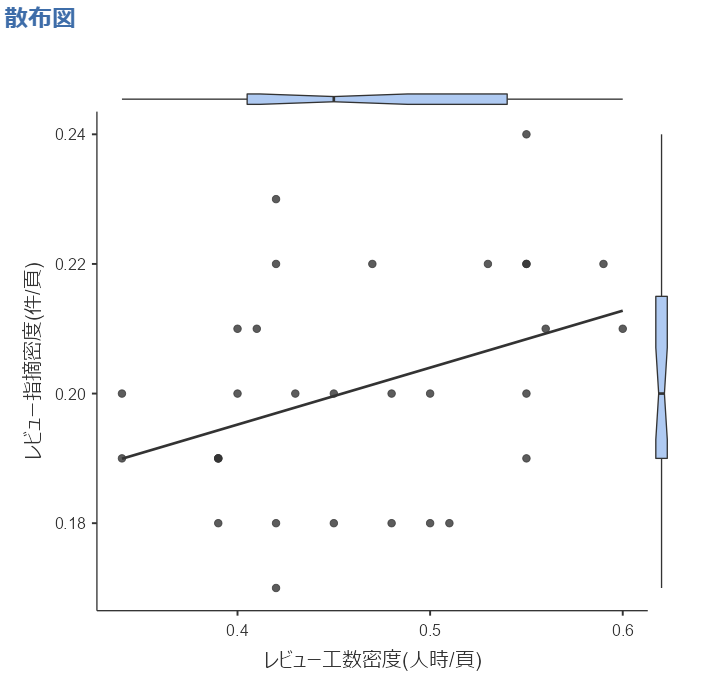
描画しなおした散布図&箱ひげ図は以下のようになりました。
散布図単独だとデータの偏りや傾向が分かりづらいですが、散布図と箱ひげ図を一緒に描画することによって、データの”偏り”、”傾向”の把握が容易になりました。
散布図を、箱ひげ図の第1四分位数、第2四分位数(中央値)、第3四分位数で点線で区切ってみましょう。
(jamoviでは図中の区切り線は描画してくれないので、図を画像にしてExcel等に貼り付けて手動で描画しています)
どのエリアに何点くらいデータがあるのか大まかに把握できるようになりました。
このように箱ひげ図と散布図を組み合わせることで、簡単にデータを層別して”視覚的”に確認することができます。
jamoviを使えばデータを設定してメニューから機能を選択するだけで描画は完成です。とてもお手軽に結果を得ることができます。
まとめ
#散布図に箱ひげ図を一緒に描画することで
- 最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値の関係を把握しやすくなる。
- 分布の偏りを把握しやすくなる。
- データを層別しやすくなる。
などの効果があることがわかりました。
次回は、データの「層別」から見えてくる品質観点を詳しくみていきたいと思います。
データ分析に活用して頂ければ幸いです。