はじめに

ボイドモデルという人工生命モデルを知っていますか？
人工生命と言われると、なにやら高度な技術を使って生命を作り出すような感じがしますが、調べてみるとどうやら鳥の動きを再現するシミュレーションのようです。

しかも割と簡単なプログラミングでできるっぽい！

本物の鳥は頭脳があるのであくまで動きを再現するだけですが、
ちょっと試してみたいと思い今回は以下の文献を参考にして、PyGameでボイドモデルをシミュレーションしてみました。

Processing でグラフを描く㉑　ボイドモデル

ほとんど（というか全く？）ロジックは変わらないのですが、
PyGameによるいい感じの日本語の文献が（私が調べた限り）見つけられなかったので私の備忘がてら紹介します。
最後までお読みいただければ幸いです。

ボイドモデルとは

ボイドモデルは、アメリカのアニメーション・プログラマであるクレイグ・レイノルズが考案・作成した人工生命モデルです。「ボイド（Boids）」とは、bird-old、つまり「鳥っぽいもの」を意味する造語で、以下の３つの簡単なルールから群れを作り出すことができるアルゴリズムです。

集合（cohesion）：群れの中心に向かう
分離（separation）：ぶつからないように距離を取る
整列（alignment）：周りの鳥の動きと同じ方向に動く

これらルールを組み合わせることで、コンピュータ上の鳥たちは驚くほど自然な動きをします。
レイノルズの提案後、ボイドモデルには、より複雑で生命らしい動きを生み出すための様々な改良が加えられています。例えば、群れを作る時に恐怖といった感情を組み込んだモデルや、実際の鳥の群れのように外からの危険を察知した鳥がリーダーとなり、群れを危険から避ける力を導入したモデルが提案されています。
今回は簡単に、上記の３つのルールを加えただけのモデルを再現しました。

PyGameによるボイドモデルのシミュレーション

とりあえず自由に動かしてみる。

まずは何もルールを設定せずに、とりあえず鳥の群れを自由に動かしてみます。
ディレクトリ構成は以下の通りです。

boid/
│   main.py
└───model
        __init__.py
        bird.py

main.pyが実行ファイルで、bird.pyが一匹の鳥に対するクラスファイルです。bird.pyに鳥単体の初期値や行動ルールを定義します。
それぞれのソースコードは以下のようになっています。

bird.py

import pygame
import random
import numpy as np

RANGE_OF_DIRECTIONS = [0, 360]
BIRD_COLORS = [
	'#FFA5CC',  # pink
	'#80FF25',  # green
	'#A0D4FF',  # skyblue
]

class Bird:
	def __init__(self, bird_id, width, height):
		self.bird_id = bird_id
		self.width = width
		self.height = height
		self.direction = random.uniform(
			np.radians(RANGE_OF_DIRECTIONS[0]),
			np.radians(RANGE_OF_DIRECTIONS[1])
		)  # ランダムな初期の角度
		# 位置と速度ベクトル
		self.position = np.array([random.uniform(0, width), random.uniform(0, height)])
		self.velocity = np.array([np.cos(self.direction), np.sin(self.direction)])
		# 加速度ベクトル
		self.acceleration = np.array([0, 0])
		self.acceleration_to_cohere = np.array([0, 0])
		self.acceleration_to_separate = np.array([0, 0])
		self.acceleration_to_align = np.array([0, 0])
		# 鳥の形状
		self.polygon = np.array([(20, 0), (0, 5), (0, -5)])
		self.type_id = self.bird_id % 3
		self.color = BIRD_COLORS[self.type_id]

	def move(self):
		self.position += self.velocity
		
		# 鳥が壁にぶつかったら反対側に通り抜ける
		if self.position[0] > self.width or self.position[0] < 0:
			self.position[0] = np.abs(self.position[0] - self.width)
		if self.position[1] > self.height or self.position[1] < 0:
			self.position[1] = np.abs(self.position[1] - self.height)

	def display(self, screen):		
		# 回転行列を形成
		rotation_matrix = np.array([[np.cos(self.direction), -np.sin(self.direction)],
									[np.sin(self.direction), np.cos(self.direction)]])
		# 頭を進行方向にするように回転させる。
		rotated_polygon = np.dot(self.polygon, rotation_matrix.T) + self.position
		pygame.draw.polygon(screen, self.color, rotated_polygon, 0)

main.py

import pygame
import numpy as np
from model.bird import Bird

# 群れの総数
BIRD_NUM = 100

# メイン実行
def main():
	pygame.init()
	# 画面サイズの設定
	width, height = 800, 600
	screen = pygame.display.set_mode((width, height))
	pygame.display.set_caption("Boid Simulation")

	# 鳥の生成
	bird_list = []
	for i in range(BIRD_NUM):
		bird_list.append(Bird(i, width, height))

	clock = pygame.time.Clock()

	# 実行
	while True:
		for event in pygame.event.get():
			if event.type == pygame.QUIT:
				pygame.quit()
				exit()
		
		# それぞれの鳥の動き
		for bird in bird_list:
			# 行動
			bird.move()

		screen.fill((0, 0, 0))

		# 鳥を描画する
		for bird in bird_list:
			bird.display(screen)

		pygame.display.flip()
		clock.tick(30)

if __name__ == '__main__':
	main()

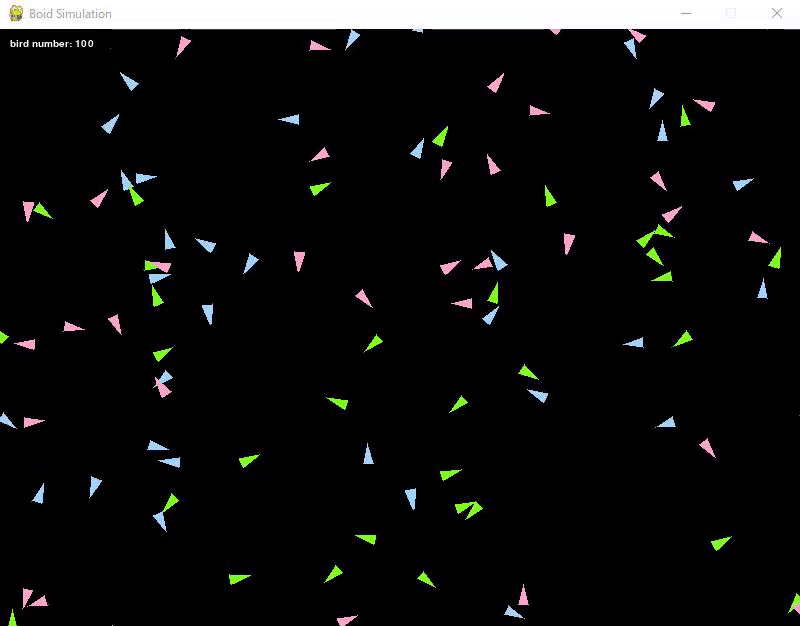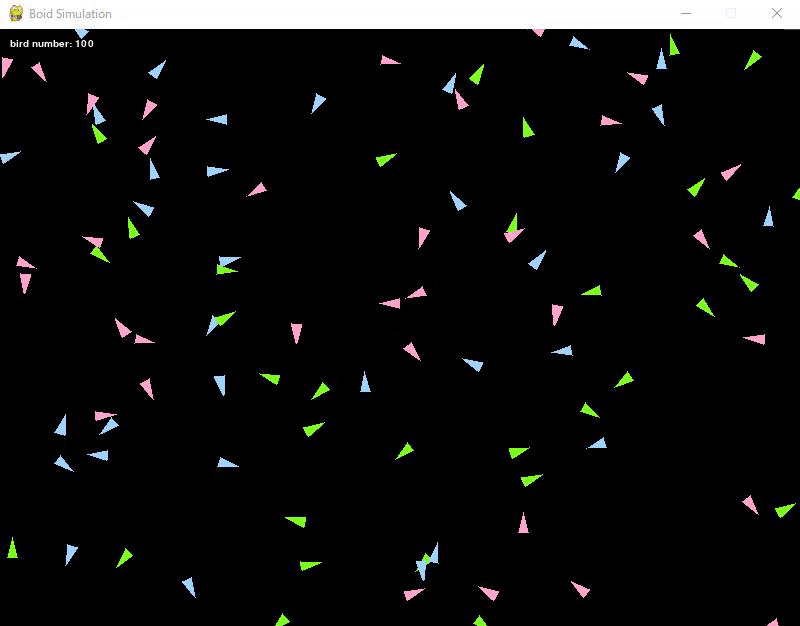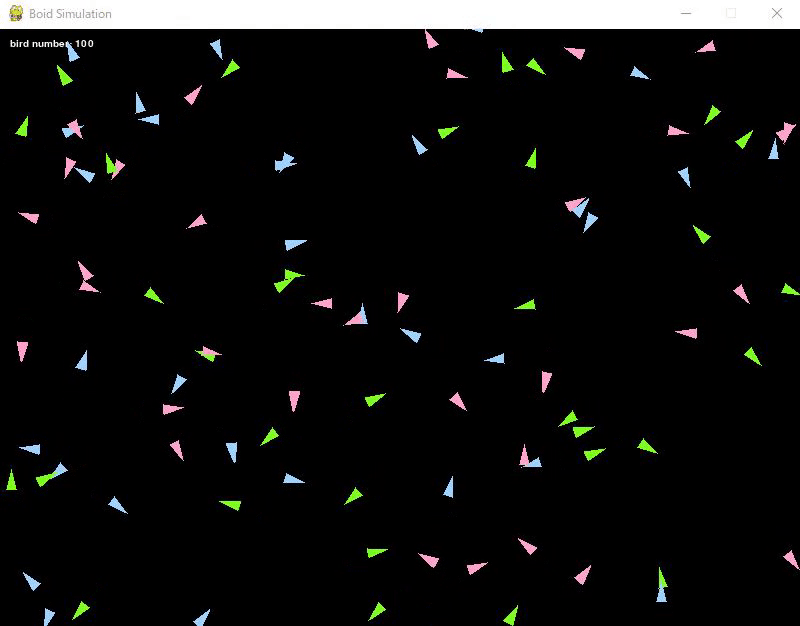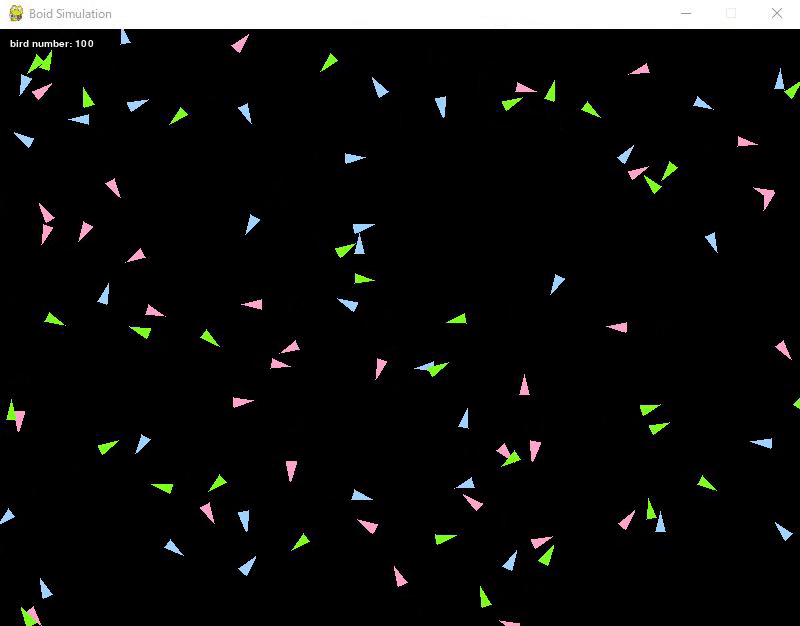
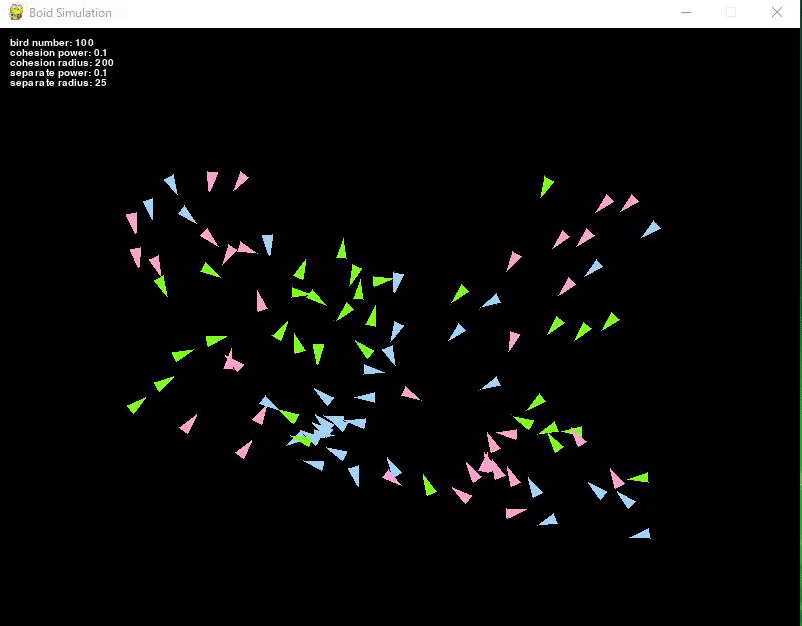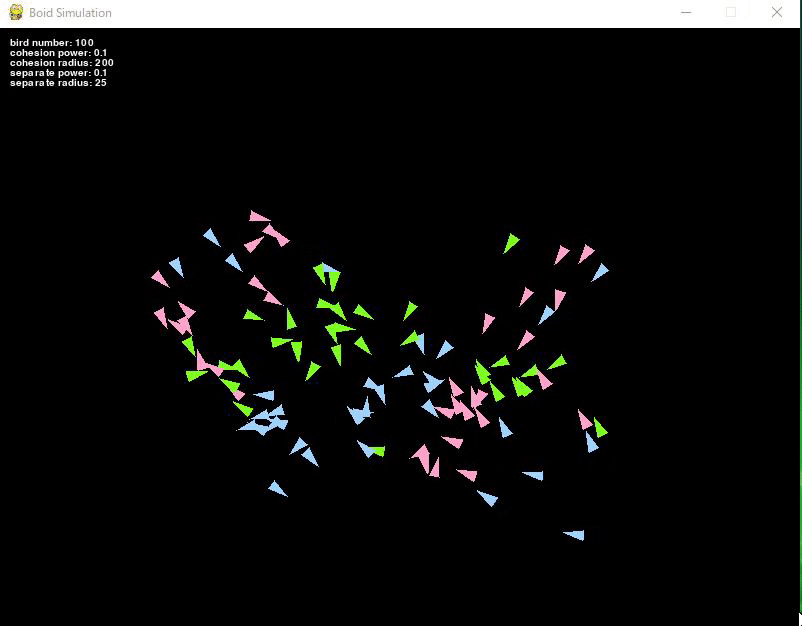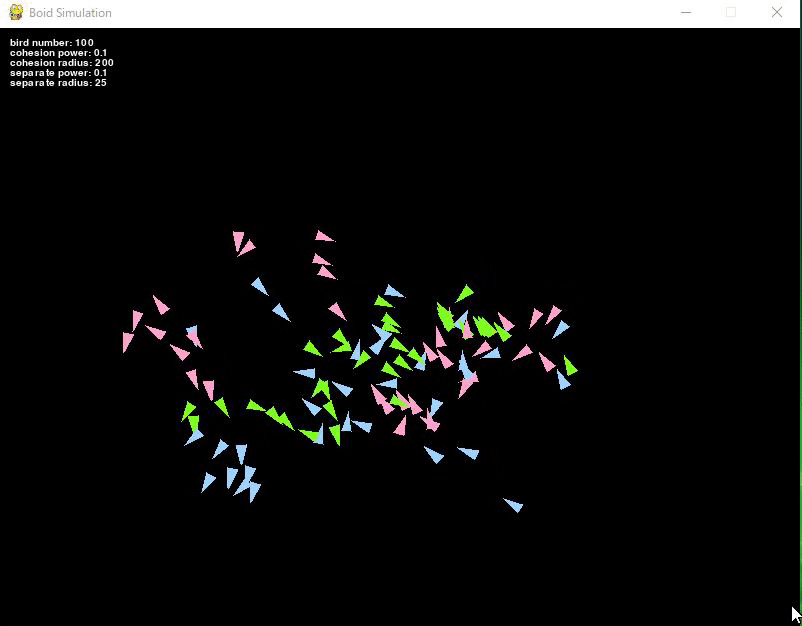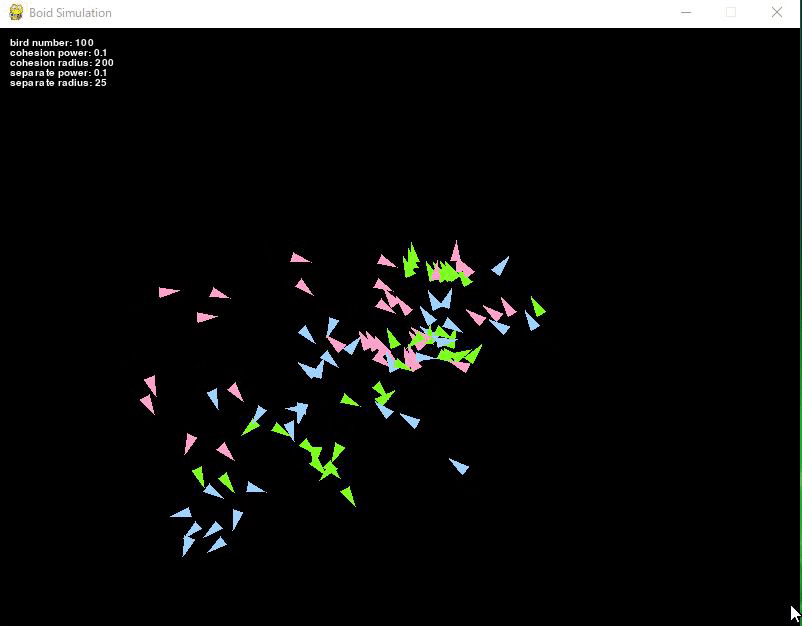
100匹の鳥を用意し、それぞれの鳥の初期値として位置と方向をランダムに設定しました。
また試しに鳥たちを３種類に色分けをしてみました。
鳥たちは、初めに決められた方向へ一直線に動き続けます。
この状態では、鳥同士は干渉し合わないのでそれぞれ好き勝手な方向に動いています。
ちなみに壁に対してはすり抜けて反対側に現れるように実装しています。

以下が実行結果です。

集合ルールの追加

では次に集合ルールのみを追加してみます。
集合する場合に、どれくらいの半径以内の鳥が集合するか（RADIUS_OF_COHERE）、群れに向かう時の力（POWER_OF_COHERE）を設定します。
ほぼ上記ソースコードと同じなので、割愛して追加した部分のみをお見せいたします。

bird.py

class Bird:
	# moveメソッドを修正修正
	def move(self):
		# 加速度ベクトルを求める。
		self.acceleration = self.acceleration_to_cohere + self.acceleration_to_separate + self.acceleration_to_align
		
		# 加速度ベクトルと速度ベクトルの和から進行方向を求める。
		vector = self.velocity + self.acceleration
		self.velocity = (vector) / np.linalg.norm(vector)
		self.direction = np.arctan2(self.velocity[1], self.velocity[0])
		self.position += self.velocity
		
		# 鳥が壁にぶつかったら反対側に通り抜ける
		if self.position[0] > self.width or self.position[0] < 0:
			self.position[0] = np.abs(self.position[0] - self.width)
		if self.position[1] > self.height or self.position[1] < 0:
			self.position[1] = np.abs(self.position[1] - self.height)
	
	# 以下のルールを追加
	# 集合ルール
	def cohere(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 近くの群れの重心ベクトル
			center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
			# 自分と群れの重心ベクトルの差
			vector = np.subtract(center_of_near, self.position)
			# 群れの重心ベクトルに向かうように加速度を計算
			self.acceleration_to_cohere = power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_cohere = np.array([0,0])

main.py

# 初期値を追加
# 集合ルール
POWER_OF_COHERE = 0.1
RADIUS_OF_COHERE = 200

# メイン実行
def main():
	# 省略

	# 実行
	while True:
		# 省略

		# ２匹の鳥同士の距離と方向
		distances_list = distances_of_vectors([bird.position for bird in bird_list]) # 追加
		# それぞれの鳥の動き
		for bird in bird_list:
			# 集合
			bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE) # 追加
			# 行動
			bird.move()

		# 省略

# メソッドを追加
# ベクトル間の距離を格納する二次元リストを生成
# 行列の各要素(i,j)には、ベクトルvector[i]とvector[j]の距離とvector[j]のインデックスが格納される。
def distances_of_vectors(vectors):
	vector_num = len(vectors)
	distance_list = [[0] * vector_num for _ in range(vector_num)]
	for i in range(vector_num):
		distance_list[i][i] = (0, i)
		for j in range(vector_num):
			if i < j:
				# ふたつのベクトルの距離を求める。
				distance = np.linalg.norm(np.subtract(vectors[i], vectors[j]))
				# i,jインデックスに求めた距離を格納する。
				distance_list[i][j] = (distance, j)
				distance_list[j][i] = (distance, i)
	return distance_list

今回は集合ルールを追加した上で、同じ色の鳥たちが集合するようにしました。
鳥の速度は加速度によって方向が変わり、同じ色の鳥たちが集合していきます。

分離ルールの追加

集合ルールのみを追加した場合、鳥の群れは小さくなりすぎて密集してしまいました。
そのため密集しないように分離ルールを追加します。
分離ルールも集合ルールと同じように、どれくらいの半径にいたら鳥が分離するか（RADIUS_OF_SEPARATION）、群れから離れる時の力（POWER_OF_SEPARATION）を設定します。

bird.py

class Bird:
	# 分離ルールを追加
	def separate(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 近くの群れの重心ベクトル
			center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
			# 自分と群れの重心ベクトルの差
			vector = np.subtract(center_of_near, self.position)
			# 群れの重心ベクトルから離れるように加速度を計算
			self.acceleration_to_separate = - power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_separate = np.array([0,0])

main.py

# 初期値を追加
# 分離ルール
POWER_OF_SEPARATE = 0.1
RADIUS_OF_SEPARATE = 25

# メイン実行
def main():
	# 省略

	# 実行
	while True:
		# 省略

		# それぞれの鳥の動き
		for bird in bird_list:
			# 集合
			bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE)
			# 分離
			bird.separate(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE) # 追加
			# 行動
			bird.move()

		# 省略

ロジックとしては集合ルールとほぼ同じで、ある半径以内にいる同じ色の鳥を抽出して、その群れと今いる位置から加速度を計算します。
集合ルールと違う点としては、加速度の計算の際に「群れから離れる」ようにするため、マイナス記号を付与しています。
これによって、群れから反対の方向に鳥が離れるようになりました。
最後に「整列ルール」を追加していきます。

整列ルールの追加

bird.py

class Bird:
	# 整列ルールの追加
	def align(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 群れの進行方向を求める
			vector = np.sum([bird.velocity for bird in near_bird], axis=0)
			# 自分が群れの進行方向になるように加速度を計算
			self.acceleration_to_align = power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_align = np.array([0,0])

main.py

# 初期値を追加
# 整列ルール
POWER_OF_ALIGN = 0.1
RADIUS_OF_ALIGN = 100

# メイン実行
def main():
	# 省略

	# 実行
	while True:
		# 省略

		# それぞれの鳥の動き
		for bird in bird_list:
			# 集合
			bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE)
			# 分離
			bird.separate(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE)
			# 整列
			bird.align(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE) # 追加
			# 行動
			bird.move()

		# 省略

整列ルールを加えると、更に動きが自然になりました。
整列ルールは、ある半径以内にいる鳥の群れと同じ方向に動くというものです。
色ごとにルールを適用しているので、青、緑、ピンクのグループが整列してそれぞれの方向に飛ぶように見えます。
（※動画時間が短いので整列していないように見えるかもしれませんが、しばらく放置していると整列して飛んでいく様子が見られます。）

まとめ

今回はPyGameを利用して単純なボイドモデルのシミュレーションを実施しました。
ボイドモデルは色々と応用ができそうで、なおかつパラメータが７つあるので各パラメータを調整することで様々な実験ができそうです。
個人的にはこのモデルを拡張して、餌を置いた時や繁殖や寿命を設定する、遺伝的アルゴリズムと組み合わせてシミュレーションしてみるなどもできたら面白そうです。

最後に３つのルールを加えた全体のソースコードを紹介します。
ぜひ試してみてください。

ソースコード

ディレクトリ構成

boid/
│   main.py
└───model
        __init__.py
        bird.py

全体ソースコード

bird.py

import pygame
import random
import numpy as np

RANGE_OF_DIRECTIONS = [0, 360]
BIRD_COLORS = [
	'#FFA5CC',  # pink
	'#80FF25',  # green
	'#A0D4FF',  # skyblue
]

class Bird:
	def __init__(self, bird_id, width, height):
		self.bird_id = bird_id
		self.width = width
		self.height = height
		self.direction = random.uniform(
			np.radians(RANGE_OF_DIRECTIONS[0]),
			np.radians(RANGE_OF_DIRECTIONS[1])
		)  # ランダムな初期の角度
		# 位置と速度ベクトル
		self.position = np.array([random.uniform(0, width), random.uniform(0, height)])
		self.velocity = np.array([np.cos(self.direction), np.sin(self.direction)])
		# 加速度ベクトル
		self.acceleration = np.array([0, 0])
		self.acceleration_to_cohere = np.array([0, 0])
		self.acceleration_to_separate = np.array([0, 0])
		self.acceleration_to_align = np.array([0, 0])
		# 鳥の形状
		self.polygon = np.array([(20, 0), (0, 5), (0, -5)])
		self.type_id = self.bird_id % 3
		self.color = BIRD_COLORS[self.type_id]

	def move(self):
		# 加速度ベクトルを求める。
		self.acceleration = self.acceleration_to_cohere + self.acceleration_to_separate + self.acceleration_to_align
		
		# 加速度ベクトルと速度ベクトルの和から進行方向を求める。
		vector = self.velocity + self.acceleration
		self.velocity = (vector) / np.linalg.norm(vector)
		self.direction = np.arctan2(self.velocity[1], self.velocity[0])
		self.position += self.velocity
		
		# 鳥が壁にぶつかったら反対側に通り抜ける
		if self.position[0] > self.width or self.position[0] < 0:
			self.position[0] = np.abs(self.position[0] - self.width)
		if self.position[1] > self.height or self.position[1] < 0:
			self.position[1] = np.abs(self.position[1] - self.height)
	
	# 集合ルール
	def cohere(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 近くの群れの重心ベクトル
			center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
			# 自分と群れの重心ベクトルの差
			vector = np.subtract(center_of_near, self.position)
			# 群れの重心ベクトルに向かうように加速度を計算
			self.acceleration_to_cohere = power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_cohere = np.array([0,0])
	
	# 分離ルール
	def separate(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 近くの群れの重心ベクトル
			center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
			# 自分と群れの重心ベクトルの差
			vector = np.subtract(center_of_near, self.position)
			# 群れの重心ベクトルから離れるように加速度を計算
			self.acceleration_to_separate = - power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_separate = np.array([0,0])
	
	# 整列ルール
	def align(self, bird_list, distance_l, power, radius):
		# 近くの群れを抽出
		near_bird_ids = [
			d[1] for d in distance_l[self.bird_id] 
			if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
		if len(near_bird_ids) > 0 :
			near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
			# 群れの進行方向を求める
			vector = np.sum([bird.velocity for bird in near_bird], axis=0)
			# 自分が群れの進行方向になるように加速度を計算
			self.acceleration_to_align = power * (vector/np.linalg.norm(vector))
		else:
			self.acceleration_to_align = np.array([0,0])

	def display(self, screen):		
		# 回転行列を形成
		rotation_matrix = np.array([[np.cos(self.direction), -np.sin(self.direction)],
									[np.sin(self.direction), np.cos(self.direction)]])
		# 頭を進行方向にするように回転させる。
		rotated_polygon = np.dot(self.polygon, rotation_matrix.T) + self.position
		pygame.draw.polygon(screen, self.color, rotated_polygon, 0)

main.py

import pygame
import numpy as np
from model.bird import Bird

# 群れの総数
BIRD_NUM = 100
# 集合ルール
POWER_OF_COHERE = 0.1
RADIUS_OF_COHERE = 200
# 分離ルール
POWER_OF_SEPARATE = 0.1
RADIUS_OF_SEPARATE = 25
# 整列ルール
POWER_OF_ALIGN = 0.1
RADIUS_OF_ALIGN = 100

# メイン実行
def main():
	pygame.init()
	# 画面サイズの設定
	width, height = 800, 600
	screen = pygame.display.set_mode((width, height))
	pygame.display.set_caption("Boid Simulation")

	# 鳥の生成
	bird_list = []
	for i in range(BIRD_NUM):
		bird_list.append(Bird(i, width, height))

	clock = pygame.time.Clock()

	# 実行
	while True:
		for event in pygame.event.get():
			if event.type == pygame.QUIT:
				pygame.quit()
				exit()

		# ２匹の鳥同士の距離と方向
		distances_list = distances_of_vectors([bird.position for bird in bird_list])
		# それぞれの鳥の動き
		for bird in bird_list:
			# 集合
			bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE)
			# 分離
			bird.separate(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE)
			# 整列
			bird.align(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE)
			# 行動
			bird.move()

		screen.fill((0, 0, 0))

		# 画面に設定を表示
		display_rendered_text(screen)

		# 鳥を描画する
		for bird in bird_list:
			bird.display(screen)

		pygame.display.flip()
		clock.tick(30)

# ベクトル間の距離を格納する二次元リストを生成
# 行列の各要素(i,j)には、ベクトルvector[i]とvector[j]の距離とvector[j]のインデックスが格納される。
def distances_of_vectors(vectors):
	vector_num = len(vectors)
	distance_list = [[0] * vector_num for _ in range(vector_num)]
	for i in range(vector_num):
		distance_list[i][i] = (0, i)
		for j in range(vector_num):
			if i < j:
				# ふたつのベクトルの距離を求める。
				distance = np.linalg.norm(np.subtract(vectors[i], vectors[j]))
				# i,jインデックスに求めた距離を格納する。
				distance_list[i][j] = (distance, j)
				distance_list[j][i] = (distance, i)
	return distance_list

# 画面に設定を表示する
def display_rendered_text(screen):
	font = pygame.font.Font(None, 15)
	text_lines = [
		"bird number: %s" % BIRD_NUM,
		"cohesion power: %s"  % POWER_OF_COHERE,
		"cohesion radius: %s" % RADIUS_OF_COHERE,
		"separate power: %s" % POWER_OF_SEPARATE,
		"separate radius: %s" % RADIUS_OF_SEPARATE,
		"align power: %s" % POWER_OF_ALIGN,
		"align radius: %s" % RADIUS_OF_ALIGN,
	]
	rendered_lines = [font.render(line, True, (255, 255, 255)) for line in text_lines]
	text_position = (10, 10)
	for rendered_line in rendered_lines:
		screen.blit(rendered_line, text_position)
		text_position =(text_position[0], text_position[1] + rendered_line.get_height())

if __name__ == '__main__':
	main()

PyGameでボイドモデルのシミュレーションをしよう

はじめに

ボイドモデルとは

PyGameによるボイドモデルのシミュレーション

とりあえず自由に動かしてみる。

集合ルールの追加

分離ルールの追加

整列ルールの追加

まとめ

ソースコード

参考文献