Get back to where the joy of programming
はじめに
#かつて職場の同僚が、ITの現場にいる理由について、このように語っていました。
小学生の頃、プログラミングで簡単なゲームを作成しました。今思い返すと、まったくゴミみたいなプログラムだったのですが、それが動いた時、すごくうれしくて感動しました。
その原体験があるから、僕は今、ITの現場にいるのです。
その話を聞いたのは10年以上前のことですが、遠い目で語る同僚の姿をよく覚えています。
思い返せば、私自身も小学生の頃、何もわからないままに BASIC でゲームを写経したことがあります。もちろんネットもないので、限られた情報の中で試行錯誤しながら、ブロック崩しのようなものを作ったように記憶しています。
残念ながら、同僚のように原体験となるようなのもは得られませんでしたが、それでも楽しかったことは覚えています。
楽しさの根にあるもの
#楽しさや嬉しさの根には、もちろん若いからという部分が大きいですが、限られた情報しかない中で、全てをコントロールしているという全能感があったように思います。
そのように考えると、現代は不幸な時代なのかもしれません。ITは日毎に高度化し、情報は氾濫し、作ることの単純な楽しさを得る機会は日増しに少なくなっている気がします。なにを始めるにせよ、周辺ツールやフレームワークは溢れかえり、今日得た知識は直ぐに使い物になってしまいます。周辺ツールやフレームワークを使っているのではなく、それらに使われているような気さえしてきます。このような中では、全てをコントロールしているような全能感を感じる体験は、なかなかできるものでもないでしょう。
心の高ぶりを取り戻す
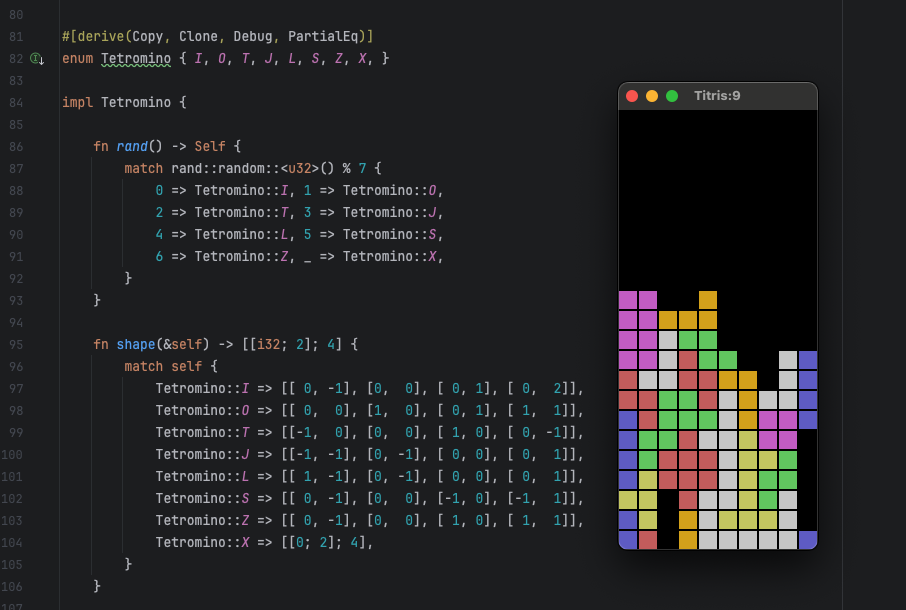
#本記事では、Rust で低レベルなテトリスのクローンを作り、あのころの心の高ぶりを取り戻してみようと思います。そして出来ることなら、プログラミング未経験者の方に、かつて同僚が感じたような喜びを体感いただけないものかと考えています。
テトリスクローン Titris
#商標の関係もあるため、アプリケーションの名前は、小さな(Tiny)テトリスということで Titris と呼ぶことにします。
Titris の実装は、簡単すぎず、複雑すぎず、だれでもルールを知っていて、なによりプレーするのが楽しいので、このような用途は最適な題材です。ただ、プログラミング未経験者の方が Rust から始めるのは少しハードルが高いのは事実です。ですので、細かなRustの文法はなんとなくの理解でも、とにかく動くプログラムを作ることで、作ることの楽しさを感じていただきたいと思います。ソースコードは、全体でも 300 行程度で済みますので、プログラムってこんな感じで動いてるのね ということは実感いただけると思います。
それでは、Titris を作るツアーに出かけましょう。
想定読者と前提事項
#本記事で想定する読者は以下の方です。
- プログラミング未経験またはそれに準じる方
- Rust 言語によるプログラミングの雰囲気をザックリ知りたい方
プログラミングの考え方と、Rust 言語の説明を合わせて行っていきますが、Rust の文法について詳細な説明には立ち入りません。まずは作って動かし、雰囲気を掴むことから始めましょう。
使用ツール
#使用するツールは以下となります。
- Rust
- コマンドプロンプトまたはターミナル
- テキストエディタ(メモ帳でも可)
Rust のインストールは事前に済んでいることを前提とします。まだインストールされていない方は、Rust をインストール などを参考にインストールを済ませておいてください。
Windows 環境で Rust を動かすには Microsoft C++ Build Tools がインストールされている必要があります。
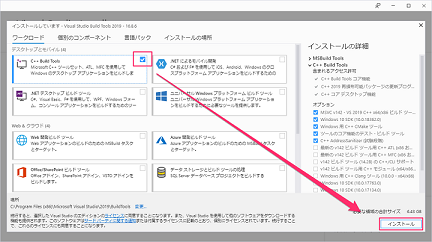
インストールされていない場合は、手順のなかで Microsoft C++ Build Tools のインストーラを起動することになりますが、何を選べば良いのかが分かりにくいと思いますのでイメージを貼り付けておきます。
C++ Build Tools だけを選択すれば十分です。
コマンドプロンプトという言葉にピンと来ない方は、Windows タスクバーの検索ボックスに cmd と入力して「コマンドプロンプト」を選択して起動してください。
本記事執筆時に利用した Rust は以下のバージョンとなっています。
> rustc --version
rustc 1.76.0 (07dca489a 2024-02-04)
> cargo --version
cargo 1.76.0 (c84b36747 2024-01-18)
使用コマンド
#本記事では、コマンドプロンプトまたはターミナルでコマンドを実行しますが、使用するのは以下の5つだけとします。
| コマンド | 内容 | 例 |
|---|---|---|
| mkdir <ディレクトリ名> | 指定の名前でディレクトリを作成する | mkdir titris |
| cd <ディレクトリ名> | 指定のディレクトリの中に移動する | cd titris |
| cargo init | 現在ディレクトリにアプリケーションのプロジェクトを作成する | cargo init |
| cargo add <クレート名> | Rust アプリケーションにクレートの依存を追加する | cargo add rand |
| cargo run | アプリケーションを実行する | cargo run |
cargo は Rust をインストールすることで使用できるようになるコマンドです。
アプリケーション作成の開始
#これから Titris を作成していきます。最初にコマンドプロンプトまたはターミナルで、アプリケーション開発用のフォルダを作成します。
以下のコマンドを実行しましょう。
mkdir titris
cd titris
ここで行ったのは、titris というフォルダの作成と、そのフォルダの中への移動です。エクスプローラやファインダなどでフォルダを作成して開くのと同じことをコマンドで行っているだけです。
次に、Rust アプリケーションを作成するためのプロジェクトを作成するため、以下のコマンドを実行しましょう。
cargo init
このコマンドは、Rust でアプリケーションを作成するために必要な雛形ファイルを自動で作成します。
コマンドを実行すると現在のディレクトリに、Cargo.toml というファイル、src フォルダの中に main.rs というファイルが作成されます。Cargo.toml は、アプリケーションの設定情報を定義するものですが、本記事では触りません。
main.rs がアプリケーションのソースコードを記載するファイルです。
クレートの追加
#これからアプリケーションを少しずつ作成していきますが、最初に少し準備を済ませておきます。cargo init を実行したのと同じ場所で、以下のコマンドを実行してください。
cargo add winit
cargo add softbuffer
cargo add tiny-skia
cargo add rand
このコマンドは、これから作成するアプリケーションで使う部品を Cargo.toml ファイルに追加します。コマンドを実行した後、Cargo.toml ファイルをテキストエディタで開けば、設定が追加されていることがわかります。
これらの部品は、クレートと呼び、インターネット上で公開されているソースコードの塊です。アプリケーションを作成する場合、必要な部品(クレート)を選んで Cargo.toml に登録することで、これから作成する自身のソースコードから利用できるようになります。全てを自分で書くことなく、既に作成された機能を自身のアプリケーションに取り込むことができるわけです。
ここで追加したクレートは以下となります。
| クレート | 説明 |
|---|---|
winit |
ウインドウを作成したり、マウス操作などのイベントを扱う |
softbuffer |
ウインドウにグラフィックスを描画する際のバッファ |
tiny-skia |
2Dグラフィックスを描画するライブラリ。円や四角形などの図形を描画することができる |
rand |
乱数を発生するライブラリ。今回は、ランダムなブロックを生成する際に利用する |
後ほど登場しますので、ここではクレートを4つ追加したことだけ覚えておけば十分です。
アプリケーションを実行してみよう
#アプリケーションを作成するための準備が整ったところで、早速プログラミングに取り掛かりましょう。
Rustでアプリケーションを作成する場合は、src フォルダの中の main.rs というファイルにプログラムを記述します。このファイルをテキストエディタで開きましょう。
既になにやら記載されています。これはソースコードの雛形を cargo init コマンドが作成してくれたものです。
fn main() {
println!("Hello, world!");
}
この雛形の段階で、アプリケーションを実行できます。
以下のコマンドを実行してみましょう。
cargo run
しばらくメッセージが出力されたあとで、以下の文字が表示されるはずです。
...
Hello, world!
何が起きたのでしょうか。
cargo run というコマンドは、ソースコードをコンパイルし、コンパイルされたファイルを他のライブラリなどとリンクし、実行可能ファイルを作成し、それを実行します。main.rs に書いた内容が、コンピュータが理解できる形に変換され、それが実行されたということだけ理解すれば十分です。これからソースコードを変更して cargo run で実行という流れを繰り返していくことになります。
Hello, world プログラムを眺める
#main.rs に書かれている内容をもう一度見てみましょう。最初の行には以下の記載があります。
fn main() {
fn というのは関数 function の略で、main という名前の関数を宣言しています。関数とは、何かしらの処理を行うソースコードの塊で、 { から } までが、この関数の定義になります。
関数は、渡された値に対して計算結果を返したり、何かしらの処理を実行できます。今回のソースコードでは、println!("Hello, world!"); という処理を実行するだけです。プログラミングは、このような関数を呼び出すことで、やりたいことを実現します。
main という名前の関数には特別な意味があります。アプリケーションを実行すると、最初にこの main関数が実行されます。つまり、この関数がアプリケーションの入口となるのです。
main 関数の中身を見てみましょう。
println!("Hello, world!");
これは、読んだ通り、Hello, world! という文字列を画面に表示せよ ということを伝えています。print!() は print line の略で、指定した文字列を末尾で改行して出力する命令です。print!() という命令もあり、こちらは改行なしで文字列を出力します。
println!() はマクロとして実装されています。Rustではマクロは末尾に ! 記号が付きます。その他 vec! マクロなどもよく使います。
println!() マクロの定義は以下のようになっています。
macro_rules! println {
() => {
$crate::print!("\n")
};
($($arg:tt)*) => {{
$crate::io::_print($crate::format_args_nl!($($arg)*));
}};
}
マクロの詳細については理解する必要はありません。コンパイル時に、マクロ呼び出しが展開され、Rust コードに置き換えられるとものだと把握していれば十分です。
アプリケーションの実装 その前に
#さて、Hello, world プログラムの内容はわかりました。続いて Titris の実装に進みたいところですが、ここで何を作ればよいのかを確認しておきましょう。
Titris の全体像
#プログラミングを行う場合、何を行おうとしているのかを理解しておくことが重要です。分かっている気になっているものでも、整理して考えてみると意外と理解が足りていないということが良くあります。今回の題材であるテトリスは、誰でも知っているような内容ですが、一度立ち止まって確認しておきましょう。
テトロミノ
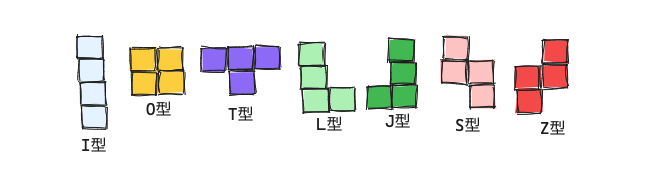
#4つの同じ大きさの正方形を辺に沿って組み合わせた多角形はテトロミノ(Tetromino)と呼びます。テトロミノは、回転操作によって形が同じになるものを同一と考えると、7つの種類があります(鏡像が同じものを同一と考えると5種類になります)。
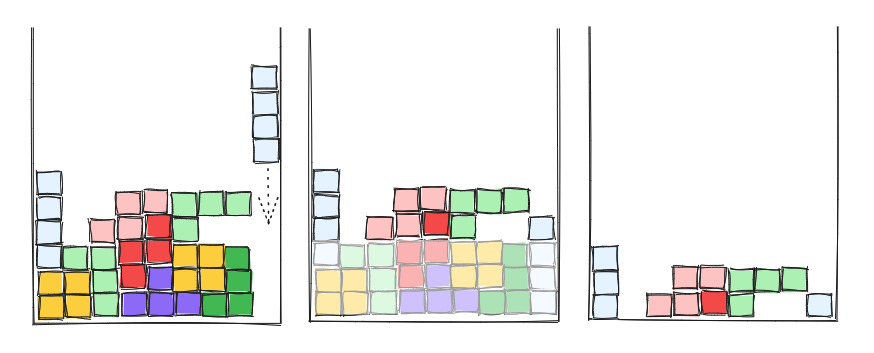
落下ブロック
#Titris では、上から落下してくるテトロミノのブロックを、左右移動と回転をさせながら盤面の中に隙間なく配置していきます。隙間なく埋めることができた行は消え、残った上段のブロックは落下します。消すことができた行数に応じて得点が入り、この得点を競います。
Titris で行うべきこと
#まとめると以下のようになります。
- テトロミノには7つの形異なった形がある
- ランダムに選択されたテトロミノ(以降ブロックと呼ぶ)を操作する
- 落下ブロックは左右移動と回転ができ、時間の経過で落下する
- 落下ブロックは盤面の外と既にブロックが存在する位置には移動できない
- 盤面上の行にブロックが隙間なく埋められた場合、行ブロックを削除して、上部のブロックは落下する
- 消すことができたブロックに応じて得点が入る
- 盤面上の(既に落下済みの)ブロックの位置を記憶しておく必要がある
やるべきことが分かったので、段階的にプログラミングを進めていきましょう。
最初にテトロミノから始めます。
テトロミノの定義
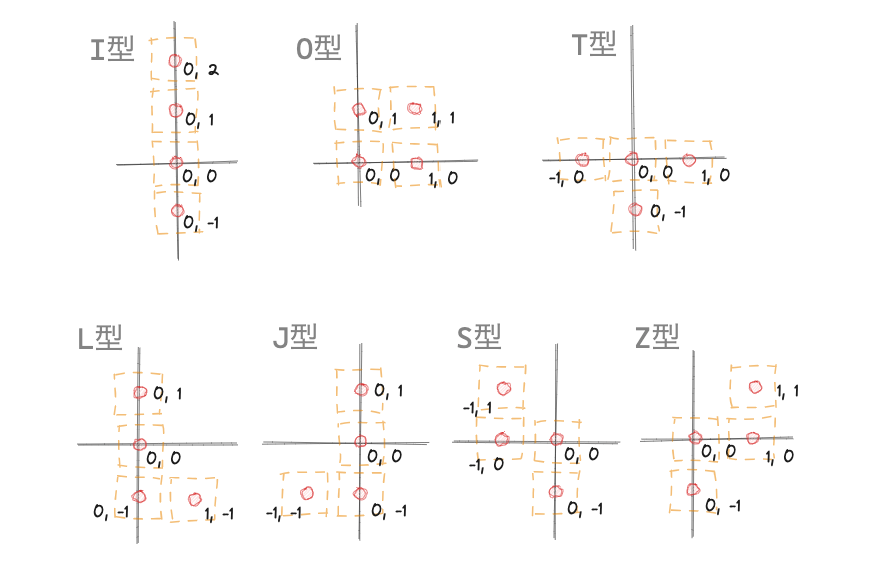
#テトロミノには、I型、O型、T型、J型、L型、S型、Z型の7つの種類があります。それぞれのテトロミノの形を2次元座標上で表すと、以下のように考えることができます。
いくつかの種類を表す場合、プログラミングでは列挙(enum)が良く使われます。
列挙とはいくつかの種類を型として定義したもので、enum キーワードにより宣言します。
main.rs ファイルに以下を追加しましょう(main 関数はそのまま残し、下段に追記すれば良いです)。
#[derive(Copy, Clone, Debug, PartialEq, Eq)]
enum Tetromino { I, O, T, J, L, S, Z, X, }
impl Tetromino {
fn rand() -> Self {
match rand::random::<u32>() % 7 {
0 => Tetromino::I, 1 => Tetromino::O,
2 => Tetromino::T, 3 => Tetromino::J,
4 => Tetromino::L, 5 => Tetromino::S,
6 => Tetromino::Z, _ => Tetromino::X,
}
}
fn shape(&self) -> [[i32; 2]; 4] {
match self {
Tetromino::I => [[ 0, -1], [0, 0], [ 0, 1], [ 0, 2]],
Tetromino::O => [[ 0, 0], [1, 0], [ 0, 1], [ 1, 1]],
Tetromino::T => [[-1, 0], [0, 0], [ 1, 0], [ 0, -1]],
Tetromino::J => [[-1, -1], [0, -1], [ 0, 0], [ 0, 1]],
Tetromino::L => [[ 1, -1], [0, -1], [ 0, 0], [ 0, 1]],
Tetromino::S => [[ 0, -1], [0, 0], [-1, 0], [-1, 1]],
Tetromino::Z => [[ 0, -1], [0, 0], [ 1, 0], [ 1, 1]],
Tetromino::X => [[0; 2]; 4],
}
}
}
追加した内容(コード)について1つずつ見ていきましょう。
列挙型 Tetromino
#最初にあるのは以下のようなコードです。Tetromino という名前の列挙型を宣言しています。
#[derive(Copy, Clone, Debug, PartialEq, Eq)]
enum Tetromino { I, O, T, J, L, S, Z, X, }
Tetromino には、I, O, T, J, L, S, Z, X という8種類のバリエーションが存在することを宣言しています。テトロミノは7種類ですが、何も存在しいない空背景を表すものとして X を加えています。後の処理でブロックの扱いを簡単にするためのものです。
列挙宣言の前には #[derive(Copy, Clone, Debug, PartialEq, Eq)] という属性を付与しています。この属性を付与することで、プログラムコードのコンパイル時に、指定した属性に応じたコードが自動で出力されます。属性はそれぞれ以下の意味を持ちます。ここでは詳細には立ち入らず、紹介だけにとどめます(あまり気にしなくて大丈夫です)。
Copy: 指定の型が Copy 型となり、代入操作が移動ではなくコピーされるようになるClone: 自分自身のコピーを作ることができるDebug:println!マクロの{:?}フォーマットで出力できるようにするPartialEq:==や!=で自身を他のインスタンスと比較できるようにするEq:全てのフィールドの同値性にて同値比較するマーカートレイト
Tetromino の実装
#Tetromino 型の宣言の後に以下のコードが続いています。これは impl により、型に対する実装を追加するコードです。
impl Tetromino {
// ...
}
Tetromino という型に対して、その型が行える機能を、{ } の中に定義します。その機能の内の1つが、以下の関数で、ランダムに Tetromino を生成する関数です。
fn rand() -> Self {
match rand::random::<u32>() % 7 {
0 => Tetromino::I,
1 => Tetromino::O,
// ...
6 => Tetromino::Z,
_ => Tetromino::X,
}
}
この関数は、rand() という名前で、この関数を呼び出すことで、 -> に続く Self、つまり自身の型である Tetromino を返すものとして定義しています。
関数は、fn 関数名(引数リスト) -> 戻り値の型 { 関数ボディ } の形式で定義します。今回の場合は、引数リストが無いので空になっています。例えば、足し算する関数を考えると fn add(a: i32, b: i32) -> i32 { a + b } のように書くことができます(i32 は32ビットの整数型を表す)。そして、add(2, 3) のように呼び出せば 5 が得られるといった具合です。
rand() 関数は(後述するように&selfを引数に取らないため)型関連関数と呼び、オブジェクト指向言語における static メソッドと考えることができます。
続く行には rand::random::<u32>() という記述があります。ここで、事前に導入しておいた rand クレートの機能を利用して乱数を得ています。::<u32> という記述は型パラメータを指定するもので、乱数が符号なしの32bit値、つまり 0 〜 4,294,967,295 までの範囲の数値が生成されます。
生成された乱数に対して、% 7 という計算を行うことで、7 で割った余りを得ています(割り算の商を得る場合は / 演算子があります)。例えば、乱数として生成された数値が 9 だった場合は、余りは 2 となります。7 で割ることで、7 以上の余りは発生しないため、結果、0から6の範囲のランダムな数値を得ることができるわけです。
rand::random::<u32>() % 7 というコードは、rand::thread_rng().gen_range(0..7) のように書くこともできます。これは rand クレートが提供する機能です。rand::thread_rng().rng.gen_range(0..=6) のように書いても同じです。
プログラミングでは、% 演算により余りを利用する場面も多いため、% を使った実装として紹介しました。
0から6 の範囲の数値は、 match とそれに続く 0 => ..., という部分(=> を match式のアームと呼ぶ)で該当するものに処理が分岐されます。ランダムな数値として 0 が得られた場合、match 式により Tetromino::I が選択され、これが関数の戻り値となります。
最後のアームは _ => Tetromino::X, のように書かれています。_ はワイルドカードパターンと呼び、何にでもマッチし、その値を無視します。なので、この場合は「上記に該当しない場合」のように読むことができます。
match による処理の分岐はパターンマッチと呼び、Rust プログラミングで頻出する書き方です。
続く shape() 関数でもパターンマッチを使っています。
fn shape(&self) -> [[i32; 2]; 4] {
match self {
Tetromino::I => [[ 0, -1], [0, 0], [ 0, 1], [ 0, 2]],
// ..
Tetromino::X => [[0; 2]; 4],
}
}
この shape() 関数は、テトロミノの4つの正方形それぞれの座標点(x, y座標)を得るための関数です(先に示した図の座標点の定義となります)。
shape(&self) の引数である &self は、自分自身の参照を意味します。先ほどの rand()は、Tetromino という型に関連付けられた関数で、型関連関数と呼びますが、こちらは型のインスタンスに対して呼ぶことができるメソッドです。メソッドは、第1引数に自身のインスタンスの参照である &self を受け取ります。
型関連関数を呼び出す場合は、Tetromino::rand() のように型に対して関数呼び出します。一方メソッドの場合は、tetromino.shape() のように、型のインスタンスに対して呼び出します。関数の呼び出しについては後述するので、ここで先に進みましょう。
Rust の符号無し整数型は、u8 u16 u32 u64 u128 usize があり、符号付き(マイナスを含む)整数型は、i8 i16 i32 i64 i128 isize があります(末尾の数字はビット数、つまり格納できる数の大きさを表します)。これらは「型」で、格納できる値の種類を制限しています。
let x: i32 = 6; とすると、6 という数値がメモリに配置され、x という i32 型の変数名で、その数値にアクセスできるようになります。この時の 6 という値がインスタンスです。実体のある値そのものを表します。
shape() 関数の戻り値は -> [[i32; 2]; 4] のように指定されています。これは何でしょうか。
[[i32; 2]; 4] は2次元の配列を意味します。配列とは、同じ型の数値(など)が並んだもので、ここでは x座標とy座標の数値の並び(1次元配列)が 4 つ並ぶことで2次元の配列を構成しています。
配列型は、[型; 要素数] で定義し、[i32; 2] は i32(32ビット整数)型の要素が 2 つ並ぶ型を意味します。[i32; 2] が4つ並んだものが [[i32; 2]; 4] となり、この配列で、テトロミノの形を構成する x, y 座標の並びが 4 つあることを表しています。
match self という記述は先程見てきたパターンマッチと同じです。self というのが、引数で受け取った自分自身のインスタンスであり、自身が Tetromino::I なのか Tetromino::X なのかに応じて処理を分岐します。もし自身が Tetromino::I 型であれば、[[0, -1], [0, 0], [0, 1], [0, 2]] という x, y 座標の4つの点の並びを返します。
パターンマッチの最後にある Tetromino::X => [[0; 2]; 4] は、他とは少し違う書き方になっています。これは、配列の全ての要素を同じ値で初期化する際の指定で、[初期値; 要素数]と指定します。[0; 2] とすれば、0で初期化された要素数2の配列となり、[[0; 2]; 4] とすることで、その配列が4並んだ形で初期化されます。つまり、Tetromino::X は全ての要素がゼロになります。
テトロミノを表示してみよう
#定義した Tetromino を使って、試しに画面表示してみましょう。
Tetromino には、ランダムな Tetromino を生成する関数(rand())と、形の座標点を得る関数(shape())を定義したので、この関数を使えば画面にテトロミノを出力できそうです。
main() 関数を以下のように書き換えます。
fn main() {
let tetromino = Tetromino::rand();
for y in (-2..=2).rev() {
print!("| ");
for x in -2..2 {
let mut sq = " ";
for i in 0..4 {
if tetromino.shape()[i][0] == x && tetromino.shape()[i][1] == y {
sq = "*";
};
}
print!("{}", sq);
}
println!(" |");
}
}
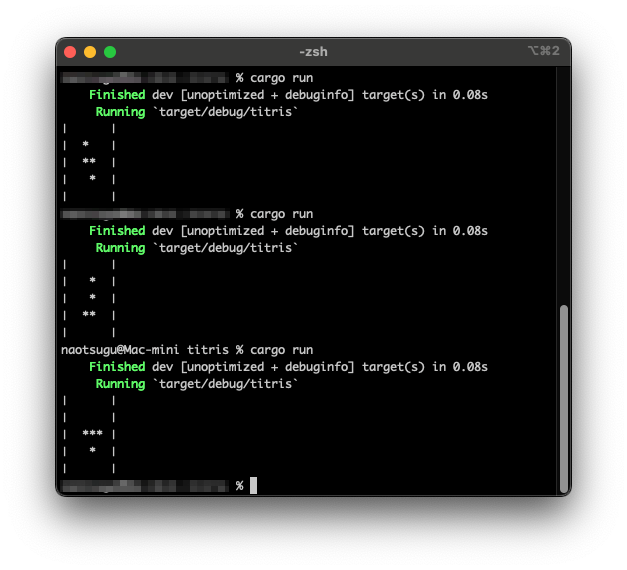
main() 関数を動かすには cargo run というコマンドを実行すれば良いのでしたね。cargo run を何回か繰り返すことで、ランダムに選択された Tetromino の形が画面に表示されることがわかります。この例では、「S型」「J型」「T型」のテトロミノが生成されたようです。
テトロミノ表示の実装
#今作成した main() 関数の中身を見ておきましょう(このmain()関数は後で消してしまうので簡単に)。
最初にあるのが以下のコードです。
let tetromino = Tetromino::rand();
関連関数により生成したランダムな Tetromino のインスタンスを、let 文により tetromino という名前の変数に割り当てています。
let 文は、ローカル変数を宣言します。通常は、let 変数名: 型 = ... の形式で : 型 を指定しますが、(Rustコンパイラが)文脈から型を推論できる場合は省略できます。この場合は Tetromino::rand() により Tetromino 型であることが明白なので、型の指定は省略できます。省略せずに書いた場合は let tetromino: Tetromino = Tetromino::rand(); となります。
let 文により、tetromino という名前のローカル変数を宣言したので、この名前を使って、ランダムに生成された Tetromino に対して操作することができます。別の言い方をすると、メモリ上に確保された Tetromino 型の値に対して、tetrominoという名前を介してアクセスできる となります。
続くコードは以下のようになっており、for ループを使った繰り返し処理を行っています。画面表示するために、x, y 座標点を1つづつ上から辿っていく処理になります。
for y in (-2..=2).rev() {
for x in -2..2 {
// ...
}
}
(-2..=2) という記述は範囲(range, ..演算子で生成する)を表し、開始..終了 のように書きます。例えば 0..5 とすれば、0から初めて、5に満たない数値、つまり0, 1, 2, 3, 4 が順に生成され、これを for ループにて順番に処理できます。5 を含めたい場合は 0..=5 のように指定します。
上記では (-2..=2).rev() のように記載しており、これは、-2, -1, 0, 1, 2 の並びを rev() で逆転させて使うことを意味します。ここでは、y座標の高い点から低い点までを順にループしています。ループ中の現在の座標値は、y という変数を介して利用できます。
次の行では、再び for ループがあり、ネストした形になっています。for x in -2..2 というループは、x座標を -2 から初めて 2 まで順にループするため、2次元座標の左上から始め、横方向に見ていき、それが終わると、外側のループで1行下がり、再び横方向に見ていきます。
for ループの中身では以下のような処理を行っています。
let mut sq = " ";
for i in 0..4 {
if tetromino.shape()[i][0] == x && tetromino.shape()[i][1] == y {
sq = "*";
};
}
これは、左上から座標を走査していく過程で、ループ中のx座標とy座標が、tetromino の4つの正方形の座標位置に一致した場合 * 印を設定するということを行っています。
let mut sq = " "; は、mut キーワード(mutable(可変)の略)が付いた変数宣言です。mut を付けた変数は可変となり、変数に値を再度代入できるようになります(反対に mut キーワードを付けない場合は、再代入することはできません)。" " はブロックが存在しないことを意図したものです。ブロックが存在する場合、この変数 sp に * 印を再代入しようというわけです。
テトロミノは4つのブロックで構成されるため、これらの座標を1つずつ for i in 0..4 { ... } ループで検査します。
tetromino.shape()[i][0] == x では、テトロミノのi 番目の正方形のx座標の一致を調べており、tetromino.shape()[i][1] == y では y 座標の一致を調べています。tetromino.shape() は戻り値として2次元配列を返すので、その配列の中身を [i][0] のように場所を指定して取り出しています。例えば let array = [2, 4, 8] のような配列があった場合、array[0] とすることで 2 を取り出せますし、array[2] とすることで 8 を取り出せます。これと同じことを2次元配列に対して行っているのが tetromino.shape()[i][1] の意味するところです。
値が一致するかどうかを調べるには == 演算を使います。一致した場合、true、一致しなかった場合は false となります。ここでは2つの比較を && により and 条件で連結しているため、2つの比較結果が両方とも true の場合に true となります。比較結果は if 式を使うことで場合分けを行います。比較結果が true の場合にだけ、続く { } の中の処理が実行されます。ここではブロックの存在を表す * を設定しています。
設定したブロックは print!("{}", sq); として画面に出力します。文字列中の {} の位置に、sp の内容(ここでは か *) が埋め込まれて画面表示されます。
ループと条件分岐とプログラミングの本質
#ここでは、for によるループ処理と、if による条件分岐を見てきました。その処理の過程で、変数への代入や比較を行い、やりたいことを実現しています。
プログラミングとは本質的に、ループと条件分岐によりコンピュータの処理を制御し、変数を介して計算を実行させることに他ならないのです。そう考えると、プログラミングに対して身構える必要なんて無いと思えるのではないでしょうか。
さて、テトロミノは定義できたので、続いて落下ブロックについて見ていきましょう。
落下ブロックの移動と回転
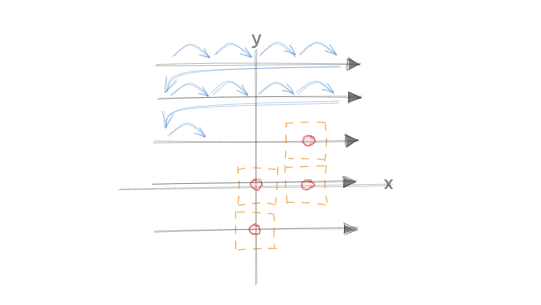
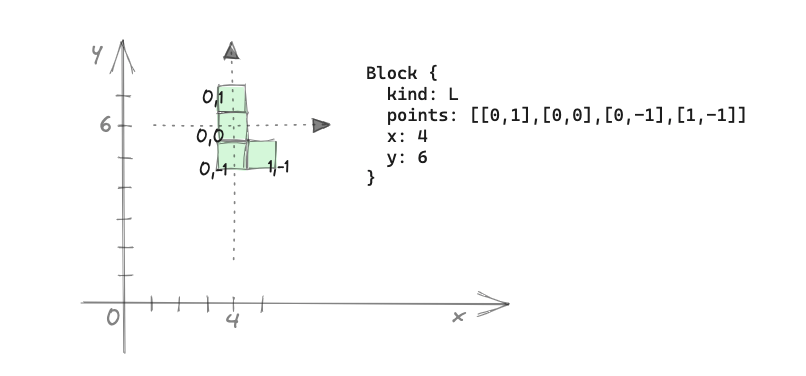
#落下ブロックは、種類(どのテトロミノか)、ブロック自身の座標系(ここではローカル座標系と呼ぶ)、親座標系におけるx座標とy座標で表すことを考えます。
Tetromino::L の種類のブロックが、4, 6 の座標に存在する場合は以下のようなイメージになります。
図中の points はブロックの各正方形の位置をローカル座標系で表したものです。この points は、初期値はテトロミノの定義から設定され、ブロックを回転させた場合に、回転に応じた座標点として書き換えられます。
親座標系におけるそれぞれのブロックの位置は、points の各点に対して、x と y の値を加算することで得ることができます。左右や下段への移動は、単に x と y の値を加算/減算することで行えます。
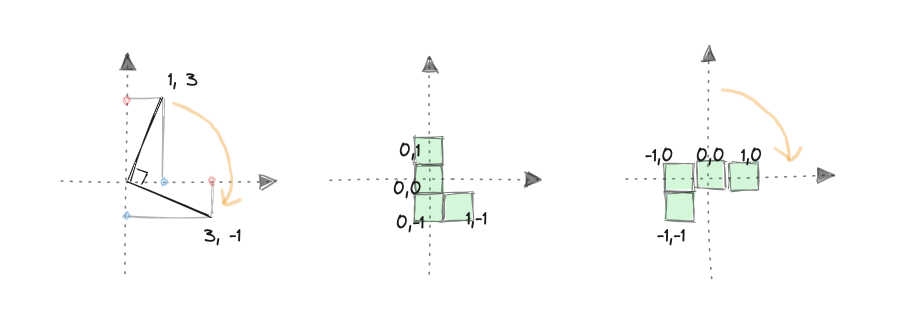
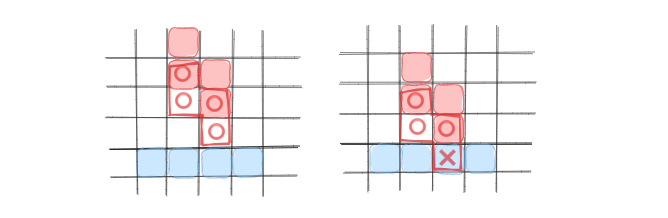
ブロックの回転についてはもう少し説明を加えましょう。ブロックは、90度毎にしか回転できないため、例えば時計回りの90度回転は、x座標とy座標を入れ替えた後で、y座標に-1 を乗じて符号を反転させるだけで済みます。
反時計周りの90度回転の場合は、こちらもx座標とy座標を入れ替えた後で、こんどは x 座標に -1 を乗じて符号を反転させればよいです。
それでは、このブロックをコードに落としてみましょう。
#[derive(Copy, Clone, Debug)]
struct Block {
kind: Tetromino,
points: [[i32; 2]; 4],
x: i32, y: i32,
}
impl Block {
fn new(x: i32, y: i32) -> Self {
let kind = Tetromino::rand();
Block {
kind,
points: kind.shape(),
x,
y: y - kind.shape().iter().max_by_key(|p| p[1]).unwrap()[1],
}
}
fn empty() -> Self {
let kind = Tetromino::X;
Block { kind, points: kind.shape(), x: 0, y: 0 }
}
fn is_empty(&self) -> bool { self.kind == Tetromino::X }
fn point(&self, i: usize) -> (i32, i32) {
(self.x + self.points[i][0], self.y + self.points[i][1])
}
fn left(&self) -> Block { Block { x: self.x - 1, ..*self } }
fn right(&self) -> Block { Block { x: self.x + 1, ..*self } }
fn down(&self) -> Block { Block { y: self.y - 1, ..*self } }
fn rotate_right(&self) -> Block { self.rotate(true) }
fn rotate_left(&self) -> Block { self.rotate(false) }
fn rotate(&self, clockwise: bool) -> Block {
let mut points: [[i32; 2]; 4] = [[0; 2]; 4];
for i in 0..4 {
points[i] = if clockwise {
[self.points[i][1], -self.points[i][0]]
} else {
[-self.points[i][1], self.points[i][0]]
};
}
Block { points, ..*self }
}
}
最初にあるのが、構造体の定義です。構造体は struct により定義し、複数の型を1つの構造として新しい型にまとめ、それに名前を付けることができます。
#[derive(Copy, Clone, Debug)]
struct Block {
kind: Tetromino,
points: [[i32; 2]; 4],
x: i32,
y: i32,
}
Block という名前の構造体を定義し、4つのフィールド(要素)を束ねています。すなわち、テトロミノの種類、各正方形の座標配列、親座標上のブロックの x 座標とy座標です。
#[derive(Copy, Clone, Debug)] 属性を付与しているため、この構造体は値としてコピーでき、さらに println!("{:?}", block) のようにデバッグ出力できます。
Block の実装
#構造体には impl で実装を追加できます。列挙 Tetromino で見たものと同じですね。
最初に定義しているのが new(x: i32, y: i32) -> Self という関数です。
impl Block {
fn new(x: i32, y: i32) -> Self {
let kind = Tetromino::rand();
Block {
kind,
points: kind.shape(),
x,
y: y - kind.shape().iter().max_by_key(|p| p[1]).unwrap()[1],
}
}
// ...
new(x: i32, y: i32) という関数は、引数に &self を含まないため、Block 構造体の関連関数です。戻り値は Self となっており、Block 型の新しいインスタンスを生成する関数になります。これはオブジェクト指向言語におけるコンストラクタと同じものです。
new() 関数は2つの引数を受け取ります。1つは x: i32 、もう1つは y: i32 です。いずれも 32bit の整数型で、ブロックの初期値位置の x, y 座標を意味します。おそらくは、x は盤面の中央位置、y は盤面の上端位置となり、その後少しずつ落下していくことになるのでしょう。
let kind = Tetromino::rand(); で、ランダムに生成した Tetromino のインスタンスを kind という変数に割り当てています。続く行では Block { ... } というコードで、新しい Block を生成しています。構造体の各要素名に割り当てる値を指定することで新しい Block を生成することができます。
ここで、構造体生成の省略記法を使っていることに注意してください。通常、kind: kind, のように構造体のフィールド名とそれに続いて設定値を指定しますが、同じ名前の場合は kind: の記述を省略できます(x, という記述でも同じ省略記法を使っています)。
さて、y - kind.shape().iter().max_by_key(|p| p[1]).unwrap()[1], というコードは意味が分からないのではないでしょうか。このコードが意図することは、テトロミノのいずれかのブロック位置が y 座標の上端をはみ出す場合は、その分を下にずらして設定するということを行っています。
テトロミノの正方形の座標を1つづつ辿り(itre())、y座標の最大値を選択し(max_by_key(|p| p[1]))、その結果(Option型)から値を取り出し(unwrap())、その正方形座標のy座標を取り出す([1])という内容です。
同じことは for ループを使って書くことも出来ます。
fn max_y(&self) -> i16 {
let mut ret = self.points[0][1];
for i in 0..4 {
ret = std::cmp::max(ret, self.points[i][1]);
}
ret
}
このコードの最終行は ret となっており、セミコロン;が付いていないことに気づいたでしょうか。Rust では、関数のボディがセミコロンなしの式で終わる場合、その式が関数の返り値となります。他の言語と同じように return ret; のように明示的に指定できますが、通常はセミコロンの有無で書き分けます(これまで見てきたコードも全て、関数の最後の式にセミコロンは置かず、戻り値としています)。
.max_by_key(|p| p[1]) の引数に指定しているのは、クロージャです。クロージャとは名前の無い関数のようなものです。関数では引数は () で括って受け取りますが、Rust のクロージャでは入力変数を|| で括ります。クロージャのボディが単一式の場合は、ブロック{ ... } を省略できます。省略せずに書くと、 |引数: 引数型| -> 戻り値型 { ボディ }; のような形になります。
クロージャについてはさらに話題がありますが、ここでは説明を省きます。興味のある方は、クロージャ: 環境をキャプチャできる匿名関数などを参照してください。
.max_by_key(|p| p[1]) は戻り値として Option を返します。Option は enum で、Some(T) または None のいずれかとなります。最大値を選択する際に、値がなかった場合は None となり、値があった場合は、Some(T) の中に値が格納されたものとなります。unwrap() は、Option から値を取り出す操作となり、値が存在しない場合はパニックとなりプログラムは終了します。通常は、None かどうかを調べて適切な処理を行いますが、ここでは値があることが分かっているため、横着して unwrap() で値を取り出しています。
同じようなものに Result があります。こちらは Ok(T) または Err(E) のいずれかとなります。入出力などの、失敗する可能性のある操作では Result が戻り値となります(Rust では例外が無い代わりに Result を使います)。Resultに対してもエラーではないことを前提に、横着して unwrap() で値を取り出すことができますが、通常は以下のようにパターンマッチを使うなどしてエラー時の処理を記述します。
match result {
Ok(ret) => { ... }
Err(err) => { ... }
}
Block 構造体の次の関数に戻りましょう。
続く関数は空ブロックを生成します。
fn empty() -> Self {
let kind = Tetromino::X;
Block { kind, points: kind.shape(), x: 0, y: 0 }
}
Tetromino::X のブロックを生成しているだけで、特に説明は不要でしょう。
その後の関数は、ブロックの種類を判定するユーティリティ・メソッドで、自身が空ブロックかどうかを判定します。
fn is_empty(&self) -> bool { self.kind == Tetromino::X }
自身の種類を self.kind == Tetromino::X として比較した結果がそのまま戻り値になります。Tetromino を == で比較できるのは、Tetromino に属性として #[derive(PartialEq)] を指定しているためです。
続いて、同じようなユーティリティ・メソッドである point() があります。
fn point(&self, i: usize) -> (i32, i32) {
(self.x + self.points[i][0], self.y + self.points[i][1])
}
これは、指定したインデックス番号 i(ここでは 0 〜 4) に対する x 座標と y 座標のタプルを返す関数です。タプルは、n 個の任意の型の組み合わせを表現するデータ型です(ここではたまたま同じ型 i32 が2つになっています)。
配列も同じようにデータの並びを扱いますが、配列の場合は異なる型のデータを混在させることはできません。
タプルは、要素の列をカンマで区切り、() で括って定義します。Rust では、関数から複数の値を返す際にタプル型を用いることが多いです。これは後で見るように、タプルがパターンマッチで扱うのに適しているからです。
次に登場するのがブロックの移動を行うメソッド3つです。
fn left(&self) -> Self { Block { x: self.x - 1, ..*self } }
fn right(&self) -> Self { Block { x: self.x + 1, ..*self } }
fn down(&self) -> Self { Block { y: self.y - 1, ..*self } }
名前の通り、ブロックの座標を更新し、更新した新しい Block を返します。..*self は、残りの要素を *self から補うという指定です(以下の参照解決の説明参照)。
ブロックの座標移動は、x座標、またはy座標のどちらかを変更するだけでよく、残りの要素は単にコピーすれば済みます。要素を1つずつ指定する代わりに、.. という指定で、残りの部分は指定したものからコピーする という指定でコード量を削減できます。なお、このようなコピー操作ができるのは、Block に属性 #[derive(Copy, Clone)] が指定されているためです。
&x は x への参照を作ります(正確には「x への参照を借用する」となります)。この参照から値を読み出すことが出来ますが、参照先の値を書き換えることはできません。つまり変更不能な共有参照となります(&mut x は排他的な可変参照となります)。
参照は、値がメモリ上のどこにあるかを指し示しています。例えば、大きな画像ファイルをメールに添付するのではなく、格納場所のリンクだけをメールに書けば、メールボックスを圧迫せずに済みます。このリンクに相当するものが参照です。参照から値を取り出す場合は、参照 r に対して、*r とすることで、参照 r の参照先の値が取得できます。メールのリンクを開く操作と考えると良いでしょう。
let x = 10;
let r = &x; // x への共有参照
assert!(*r == 10);
なお、Rustでは、. 演算子が、必要に応じて左辺を暗黙的に参照解決するようになっています。そのため、*により明示的に参照解決するケースは多くありません。
Block の実装の最後が、回転を行うメソッドです。
fn rotate_right(&self) -> Self { self.rotate(true) }
fn rotate_left(&self) -> Self { self.rotate(false) }
fn rotate(&self, clockwise: bool) -> Self {
let mut points: [[i32; 2]; 4] = [[0; 2]; 4];
for i in 0..4 {
points[i] = if clockwise {
[self.points[i][1], -self.points[i][0]]
} else {
[-self.points[i][1], self.points[i][0]]
};
}
Block { points, ..*self }
}
最初に説明したとおり、時計回りの90度回転は、x座標とy座標を入れ替えて、入れ替えた後のy座標の符号を反転させます([self.points[i][1], -self.points[i][0]])。反時計周りの場合は、こちらもx座標とy座標を入れ替えて、入れ替えた後の x 座標の符号を反転させます([-self.points[i][1], self.points[i][0]])。
座標の入れ替えを行うコードは、末尾にセミコロン; が付いていないため、if 式の戻り値になり、直接 points[i] に代入できます。この操作を for i in 0..4 で、4つの全ての点について行い、変更した座標とともに Block { points, ..*self } で(こちらもセミコロン; なし)新しい Block インスタンスとして返しています。
ここで作成した Block はうまく機能するでしょうか?
簡易的な実装を加えて動きを見てみましょう。
ブロックを動かしてみよう
#main()関数を以下のように書き換えましょう。
入力内容に応じて Block を更新して画面表示します。簡易的な確認のため、コードは最低限の実装にとどめます。
use std::io::Read;
fn main() {
let mut block = Block::new(5,4);
print(block);
loop {
let input = std::io::stdin().bytes().next()
.and_then(|result| result.ok())
.map(|byte| byte as char)
.unwrap();
match input {
'z' => { block = block.left(); },
'c' => { block = block.right(); },
'x' => { block = block.rotate_left(); },
'q' => { break; },
_ => continue
}
print(block);
}
fn print(block: Block) {
for y in (0..5).rev() {
print!("| ");
for x in 0..10 {
let mut sq = " ";
for i in 0..4 {
let (px, py) = block.point(i);
if px == x && py == y {
sq = "*";
};
}
print!("{}", sq);
}
println!(" |");
}
}
}
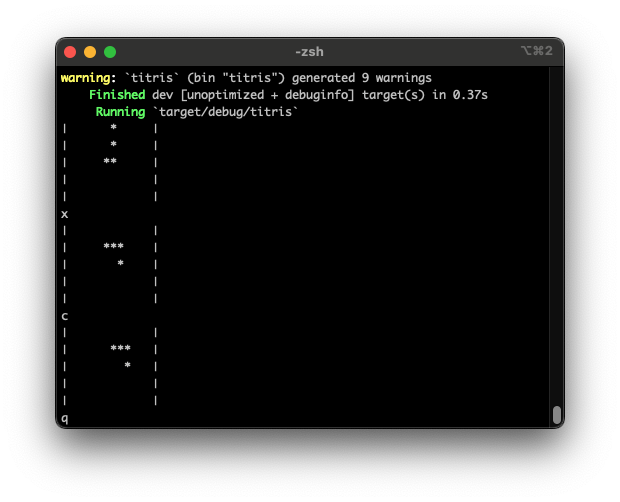
いつものように cargo で実行しましょう。
cargo run
x を入力し、Enter を押すと、反時計回りに回転したブロックが表示されます。c キーとzキーでは左右移動となります(こちらもEnter の入力が必要です)。プログラムの終了は q + Enter です。
回転や移動による座標の更新は問題なさそうですね。
main() 関数の中で、新しく登場した部分に絞って説明を加えておきます。
以下は見た目通り、ループ処理を行います。
loop {
//...
}
loop は無限にループします。ループの中で break することで、このループを脱出できます。
ループの中では、画面からのキーボード入力を受け取っています。
let input = std::io::stdin().bytes().next()
.and_then(|result| result.ok())
.map(|byte| byte as char)
.unwrap();
標準入力(std::io::stdin())からバイトのイテレータを取得し(bytes())、次のバイトを読み込み(next())、その結果から中身を取り出し(and_then(|result| result.ok()))、char 型に変換し(map(|byte| byte as char))、中身の char を取り出し(unwrap())ています。
input の内容に応じてパターンマッチでブロックのメソッドを呼び出して画面表示を行っています。
残りの部分は、ブロックを表示した時の実装と変わらないため、説明は省略します。
Block の実装が得られたので、いよいよゲームとして取りまとめる作業に入りましょう。
盤面とゲームの制御
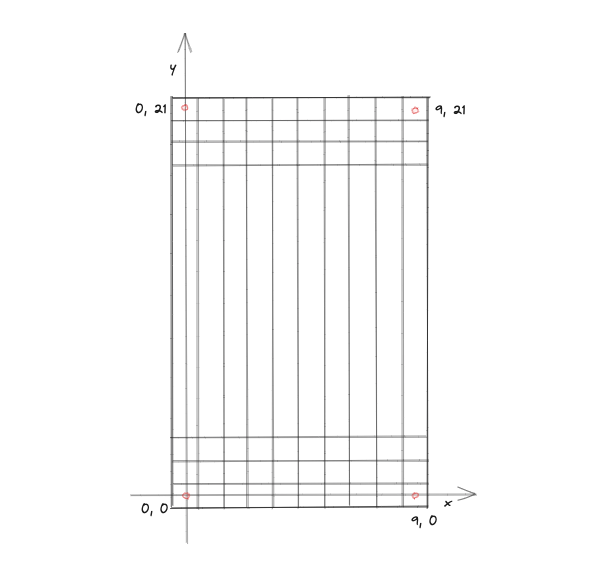
#ゲームの盤面は、横10マス、縦22マスの長方形とします。座標は左下を原点とした以下のような座標系を考えます。
盤面のマス数は 10×22 ですが、これらは配列として扱い、配列のインデックスは 0 から始まるので、最大のインデックス値は -1 した値になる点に注意してください。
定数の定義
#盤面のマス数や、その他ゲームに必要な実装を先に追加しておきましょう。
const UNIT_SIZE: i32 = 20;
const BOARD_WIDTH: i32 = 10;
const BOARD_HEIGHT: i32 = 22;
enum Key { LEFT, RIGHT, UP, DOWN, SP, OTHER, }
fn index_at(x: i32, y: i32) -> usize {
(y * BOARD_WIDTH + x) as usize
}
const は定数を定義するキーワードで、ここでは UNIT_SIZE BOARD_WIDTH BOARD_HEIGHT の3つの定数を定義しました。UNIT_SIZE は一つのマス目のサイズ(画面描画時のピクセル数)を意図したものです。
定数は値に名前をつける点で let と同じですが、const で定義した定数は、コンパイルにより定数を使うすべての場所に値が埋め込まれます。プログラムの実行時に変更しない、グローバルな値を定義する場合には const を使います。定数は全て大文字で定義することが慣例です。定数を使わず、プログラムコードに直接 22 のように書いてしまうと、変更することが困難となり、名前も付いていないので、その数字の意図することも分からなくなってしまいます。このような場合は const として定数定義するのが定石です。
続いて宣言しているのが、Key 列挙型です。これはゲーム操作で使うキーに対応したものとして利用します。
最後に index_at() というユーティリティ関数を用意しておきました。ゲームの盤面は1次元の配列で宣言するつもりなので、x, y 座標から配列のインデックスへ変換します。
ゲーム本体の実装
#ゲーム本体は以下のようになります。
すこし長いですが、Game 構造体を定義し、その実装を impl で定義している点は前述までと同じ流れです。
struct Game {
board: [Tetromino; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block,
stopped: bool,
time: std::time::SystemTime,
score: u32,
}
impl Game {
fn new() -> Self {
Game {
board: [Tetromino::X; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block::empty(),
stopped: false,
time: std::time::SystemTime::now(),
score: 0,
}
}
fn tick(&mut self) {
if self.current.is_empty() {
self.put_block();
} else if self.time.elapsed().unwrap() >
std::time::Duration::from_millis((1000 - self.score) as u64) {
self.down();
self.time = std::time::SystemTime::now();
}
}
fn put_block(&mut self) {
self.stopped = !self.try_move(Block::new(BOARD_WIDTH / 2, BOARD_HEIGHT - 1));
}
fn try_move(&mut self, block: Block) -> bool {
for i in 0..4 {
let (x, y) = block.point(i);
if x < 0 || x >= BOARD_WIDTH || y < 0 || y >= BOARD_HEIGHT {
return false;
}
if self.board[index_at(x, y)] != Tetromino::X {
return false;
}
}
self.current = block;
true
}
fn down(&mut self) {
if !self.try_move(self.current.down()) {
self.block_dropped();
}
}
fn drop_down(&mut self) {
while self.current.y > 0 {
if !self.try_move(self.current.down()) {
break;
}
}
self.block_dropped();
}
fn block_dropped(&mut self) {
for i in 0..4 {
let (x, y) = self.current.point(i);
self.board[index_at(x, y)] = self.current.kind;
}
self.remove_complete_lines();
if self.current.is_empty() {
self.put_block();
}
}
fn key_pressed(&mut self, key: Key) {
if self.stopped || self.current.is_empty() {
return;
}
match key {
Key::LEFT => { self.try_move(self.current.left()); },
Key::RIGHT => { self.try_move(self.current.right()); },
Key::UP => { self.try_move(self.current.rotate_right()); },
Key::DOWN => { self.try_move(self.current.rotate_left()); },
Key::OTHER => { self.down(); },
Key::SP => { self.drop_down(); },
};
}
fn remove_complete_lines(&mut self) {
let mut line_count = 0;
for y in (0..BOARD_HEIGHT).rev() {
let mut complete = true;
for x in 0.. BOARD_WIDTH {
if self.board[index_at(x, y)] == Tetromino::X {
complete = false;
break
}
}
if complete {
line_count += 1;
for dy in y..BOARD_HEIGHT - 1 {
for x in 0..BOARD_WIDTH {
self.board[index_at(x, dy)] = self.board[index_at(x, dy + 1)];
}
}
}
}
self.score += line_count * line_count;
self.current = Block::empty();
}
}
ここで山場は終わるので、頑張って少しずつ見ていきましょう。
Game 構造体
#ゲーム本体は以下のような構造体として定義しています。
struct Game {
board: [Tetromino; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block,
stopped: bool,
time: std::time::SystemTime,
score: u32,
}
board がゲームの盤面で、BOARD_WIDTH * BOARD_HEIGHT の長さを持つ Tetromino 型の配列です。Rustでは、配列やベクタの要素数は usize で表すため、as usize により型キャスト(i32からusizeへのキャスト)しています。多くのプログラミング言語と異なり、Rustでは暗黙的な型変換が行われないため、明示的なキャストが必要です(usize 型は、実行対象の計算機のアドレス空間サ イズに依存したビット数をもつ 符号なし整数で、たいていの場合は 64 ビットになります)。board 配列の中身は、最初は空白を表す Tetromino::X で埋めておき、落下済みのブロックが存在する位置に、空白以外の Tetromino を格納する予定です。どの位置にどのブロックがあるかが分かるので、盤面の色付けと、落下ブロックが移動できるかどうかを判定することができます。board は1次元の配列となるため、x, y 座標から、先に定義した index_at() で配列のインデックス位置を得る形でアクセスします。
current: Block は、現在落下中の(操作対象の)ブロックを表します。
stopped: bool はゲームが進行中か止まっているかを表すフラグです。bool 型は、true か false のいずれかとなる型です。
time: std::time::SystemTime は、落下スピードの制御のため、前回ブロックが落下した時のシステム時間を記録するものとします。
最後に score: u32 は名前の通り、得点を保持します。
Game 構造体の実装
#最初にあるのが new() 関数です。
fn new() -> Self {
Game {
board: [Tetromino::X; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block::empty(),
stopped: false,
time: std::time::SystemTime::now(),
score: 0,
}
}
既に見てきたものと同じなので、特に追加説明は不要でしょう。
注意しておきたい点は、board: [Tetromino::X; (BOARD_WIDTH * BOARD_HEIGHT) as usize] で盤面全体を Tetromino::X で満たしている点と、time: std::time::SystemTime::now() で現在時刻を初期値として設定している点です。
続く tick(&mut self) は、ゲームの時間を進める関数です。
fn tick(&mut self) {
if self.current.is_empty() {
self.put_block();
} else if self.time.elapsed().unwrap() >
std::time::Duration::from_millis((1000 - self.score) as u64) {
self.down();
self.time = std::time::SystemTime::now();
}
}
tick() 関数の引数は &mut self となっており、この関数内で、Game のインスタンスに変更を加えるため、mut を指定しています。
if self.current.is_empty() { ... } の条件式では、現在ブロックが空かどうかを判定し、空の場合は新しいブロックを追加するメソッドを呼び出しています。
続く else if { ... } は、先の if が条件を満たさない場合に限り、条件判定が行われます。ここでは、前回からの経過時間が1秒を超えていた場合にブロックの落下操作を行うための判定を行っています(std::time::Duration はRust の標準ライブラリが提供する経過時間を表す構造体です)。
スコアが上がるたびにこの落下までの時間を早くするため、1000 - self.score として経過時間を短くしていきます。500点を超えれば、0.5秒間隔でブロックが落下することになります。ブロックを落下させた後は、self.time = std::time::SystemTime::now(); でその時の時間を更新しています。
新しいブロックは put_block() により追加します。
fn put_block(&mut self) {
self.stopped = !self.try_move(Block::new(BOARD_WIDTH / 2, BOARD_HEIGHT - 1));
}
Block::new(BOARD_WIDTH / 2, BOARD_HEIGHT - 1) で盤面上部の中央位置を指定してブロックを生成し、try_move() 関数に渡しています。この関数は、指定したブロックが盤面に置くことができれば(つまり、他のブロックとぶつかったり、盤面をはみ出さなければ)、そのブロックを盤面に反映し、true を返します。指定したブロックを置くことができなければ false が変えるため、その場合は stopped = true となりゲームが停止します。
では、この try_move() 関数の中身を見てみましょう。
fn try_move(&mut self, block: Block) -> bool {
for i in 0..4 {
let (x, y) = block.point(i);
if x < 0 || x >= BOARD_WIDTH || y < 0 || y >= BOARD_HEIGHT {
return false;
}
if self.board[index_at(x, y)] != Tetromino::X {
return false;
}
}
self.current = block;
true
}
この関数は、引数で受け取ったブロックが盤面をはみ出したり、Tetromino::X 以外のブロックが存在していた場合に false を返します。この条件に合致しない場合は、そのブロックを現在のブロックとして設定して true を返します。
Block は4つの点で構成されるため、for i in 0..4 { .. } として4つの点について条件チェックを繰り返しています。
for ループの最初にある let (x, y) = block.point(i); は block.point() 関数からの戻り値を x と y という名前で展開されたタプル (x, y) として受け取っています。続く条件判定で、x と y として展開されたタプルの中身の値を利用しています。
if x < 0 || x >= BOARD_WIDTH || y < 0 || y >= BOARD_HEIGHT { ... } の判定では、ブロックの位置が盤面に収まることを確認しています。座標の値は 0 から始まるため BOARD_WIDTH や BOARD_HEIGHT と同じ値は、盤面の外となるため >= で比較する必要があることに注意してください。
続く条件式は if self.board[index_at(x, y)] != Tetromino::X { ... } のようになります。index_at(x, y) では、x座標, y座標に応じたboard配列のインデックスが取得できるため、self.board[index] として配列のインデックス位置のマスにあるブロックの種類が取得できます。 このマスにあるブロックの種類が Tetromino::X であれば配置できますが、そうではない場合は配置できないという判定になります。列挙 Tetromino を != で比較できるのは、#[derive(PartialEq)] 属性が定義されていることを忘れないでください。
ブロックを1段下に落下させる場合、落下した場合のブロックが引数としてやって来るので、このブロックの4つの座標に対して当たり判定を行っているわけです。
ブロックの左右への移動、回転や落下動作についても、次の位置までブロックが移動した場合、そのブロックを配置できるかを、同じようにチェックすればOKです。
ブロックを1段落下させる down() 関数は以下の様になっています。
fn down(&mut self) {
if !self.try_move(self.current.down()) {
self.block_dropped();
}
}
self.current.down() により、現在のブロックを1段下に移動させた新しいBlock 型のインスタンスが取得できます。これを先ほどの self.try_move() 関数で処理しています。もし移動できない場合は、最下部まで落下済みであるため self.block_dropped(); として落下完了時の処理を行います。
drop_down() 関数についてもほぼ同じで、こちらは一気に下まで落下させる時の処理です。
fn drop_down(&mut self) {
while self.current.y > 0 {
if !self.try_move(self.current.down()) {
break;
}
}
self.block_dropped();
}
while 条件 { ボディ } は、これまで見てきた for や loop と同様にループ処理を行います。条件を満たす間ボディの内容を繰り返し処理します。ここでは self.current.y > 0 の条件を満たす間、処理をループさせる式となっています。つまり、現在の落下ブロックのy座標が 0より大きければ(最下部まで達していないため)、処理を繰り返します。
それぞれのループ毎に、先に見た down() と同じ処理を行います。もしブロックが移動できなくなったら break により、while ループを脱出し、self.block_dropped(); による落下完了時の処理を行います。
落下完了時の処理である block_dropped() 関数を見てみましょう。
fn block_dropped(&mut self) {
for i in 0..4 {
let (x, y) = self.current.point(i);
self.board[index_at(x, y)] = self.current.kind;
}
self.remove_complete_lines();
if self.current.is_empty() {
self.put_block();
}
}
最初の for { ... } により、現在ブロックの各点に対して、その種類 Tetromino を盤面配列 board に設定しています。これで落下完了のブロックは、盤面のマスの中に設定されます。
remove_complete_lines() では、揃った行があればその行を消して得点を加算する処理を行います。その後、self.put_block() により新しいブロックを投入します。
remove_complete_lines() は、完成した行の削除を処理します。
少し長い関数なので、分けて見ていきましょう。
fn remove_complete_lines(&mut self) {
let mut line_count = 0;
for y in (0..BOARD_HEIGHT).rev() {
// この中は分けて解説
}
self.score += line_count * line_count;
self.current = Block::empty();
}
最初の line_count は、削除できた行数を扱う変数で、mut で宣言しています。続く for y in (0..BOARD_HEIGHT).rev() { ... } では、(rev() で範囲を逆転しているので)盤面y座標を上部から下に向かって1行ずつ処理をループしています。
self.score += line_count * line_count; ではスコアの値を加算しており、消せた行数の2乗の得点を加算しています。最後に、現在ブロックを空に設定して処理終了です。
では、盤面を上部から下に1行ずつ処理するループの中身に入っていきます。
前半部分にあるのが以下のコードで、この処理は分かりやすいと思います。
let mut complete = true;
for x in 0.. BOARD_WIDTH {
if self.board[index_at(x, y)] == Tetromino::X {
complete = false;
break
}
}
complete が現在処理している行が完成しているかどうかを表す変数です。for x in 0.. BOARD_WIDTH { ... } で現在の行を横方向に見ていき、空白行が存在した場合、行は完成していない(complete = false;)として break で横方向の走査を抜け出しています。
現在行が完成かそうでないかの判定結果は complete 変数に格納されており、これに応じて後続の処理を行います。
if complete {
line_count += 1;
for dy in y..BOARD_HEIGHT - 1 {
for x in 0..BOARD_WIDTH {
self.board[index_at(x, dy)] = self.board[index_at(x, dy + 1)];
}
}
}
最初の if complete { ... } により、完成行があった場合だけ処理を行います。つまり行の削除です。現在は盤面の1行毎に処理を繰り返しており、何行目を処理しているかは親のループ変数である y を見れば分かります。
for dy in y..BOARD_HEIGHT - 1 { では、現在の完成行から始め、上の行に向かって1行ずつ繰り返し処理を行います。for x in 0..BOARD_WIDTH { ... } で横方向(x座標)に1マスずつループし、self.board[index_at(x, dy)] = self.board[index_at(x, dy + 1)]; により、現在のマスに1段上のマスの内容をコピーしています。
これにより、消えた行より上のブロック全体が、落下したことになります。消えた行は line_count += 1; にて消えた行数分の数量を加えているため、この行数分の得点を計算できます。
ブロックの落下時の処理は完了です。最後に、ブロックの横移動と回転です。
fn key_pressed(&mut self, key: Key) {
if self.stopped || self.current.is_empty() {
return;
}
match key {
Key::LEFT => { self.try_move(self.current.left()); },
Key::RIGHT => { self.try_move(self.current.right()); },
Key::UP => { self.try_move(self.current.rotate_right()); },
Key::DOWN => { self.try_move(self.current.rotate_left()); },
Key::OTHER => { self.down(); },
Key::SP => { self.drop_down(); },
};
}
key_pressed() はキー入力があった場合に呼ばれる関数です。
最初のif により、ゲームが終わっていたり、落下ブロックが無い場合は、キー操作は無効なので return で関数を抜けています。
その後は、何度も見てきたパターンマッチです。キーの内容に応じた処理を行っています。ブロックを移動させて try_move() で盤面への配置を試みるという落下時の流れと同じですね。
お疲れさまでした。ゲームのコア部分の実装はこれで完了となり、残すはゲームの画面描画になります。この後、ウインドウを表示して画面を描画していきます。しかし、ウインドウの表示は多くの定型コードが登場し、いささか複雑ですので、細かいところには立ち入らず、ザックリと進めていきましょう。
ウインドウの表示
#ウインドウの表示は、それぞれのOS毎に決まったやり方があるため、アプリケーションを動かすOSに応じて、異なるソースコードを用意する必要があります。しかし、冒頭で導入した winit クレートを利用することで、同じソースコードで任意のOSで動作するアプリケーションを作成できます。
winit クレートの使い方の説明は、本記事の範囲外であるため、概要だけ見ていきます。
winit でウインドウを表示する場合のスケルトンコードは以下のようになります(ここで詳細を理解する必要はありません)。
use winit::event::{ Event, WindowEvent };
use winit::event_loop::{ ControlFlow, EventLoop };
use winit::window::WindowBuilder;
fn main() {
// イベントループの作成
let event_loop = EventLoop::new().unwrap();
event_loop.set_control_flow(ControlFlow::Poll);
// ウインドウの作成
let window = WindowBuilder::new()
.with_inner_size(winit::dpi::LogicalSize::new(400, 200))
.build(&event_loop) // イベントループと紐づけ
.unwrap();
// イベントループ
let _ = event_loop.run(move |event, elwt| {
// 発生したイベントに応じてパターンマッチ
match event {
// 閉じる処理
Event::WindowEvent { event: WindowEvent::CloseRequested, .. } => elwt.exit(),
Event::AboutToWait => {
// ここでアプリケーションの更新を行い、必要に応じて再描画要求する
window.request_redraw();
},
Event::WindowEvent {
window_id, event: WindowEvent::RedrawRequested
} if window_id == window.id() => {
// ここでアプリケーションの再描画処理を行う
},
_ => ()
}
});
}
このコードを実行すると、以下のようなウインドウが表示されます(特に自身で実行する必要はありません)。
ここで注目したいのは、ウインドウ・アプリケーションは、イベントループにより通知されたイベントに応答する形でアプリケーションが制御されるという点です。
マウスカーソルが動かされたり、キーが入力されたりといった操作は、全てOS側で処理されて、その内容がアプリケーションに通知されます。この通知が winit により、winitのイベントにマッピングされてイベントループに流れてきます。アプリケーションでは、このイベントの種類に応じて処理を行うことになります。ですので、処理を呼び出すのではなく、イベントにより呼び出されるという考え方になります。あなたの今目にしているウェブブラウザやテキストエディタも全て、このようなOSからのイベントに応じて処理が行われているのです。
では、画面への描画はどのように行えばよいでしょうか。
画面の描画は WindowEvent::RedrawRequested イベントに応答する形で実装します。画面描画の方法はいろいろありますが、ここでは、先に導入した softbuffer と tiny_skia により描画を行います。
ウインドウに正方形を表示する
#ウインドウに正方形を描画するサンプルコードは以下のようになります。こちらも細かく見る必要はありません。コード中のコメントだけ眺めれば十分です。
use winit::event::{ Event, WindowEvent };
use winit::event_loop::{ ControlFlow, EventLoop };
use winit::window::WindowBuilder;
use tiny_skia::{ FillRule, Paint, PathBuilder, Pixmap, Rect, Transform };
fn main() {
let event_loop = EventLoop::new().unwrap();
event_loop.set_control_flow(ControlFlow::Poll);
let window = WindowBuilder::new()
.with_inner_size(winit::dpi::LogicalSize::new(400, 200))
.build(&event_loop).unwrap();
// softbuffer を使うための準備を行い surface を取得
let window = std::rc::Rc::new(window);
let context = softbuffer::Context::new(window.clone()).unwrap();
let mut surface = softbuffer::Surface::new(&context, window.clone()).unwrap();
let _ = event_loop.run(move |event, elwt| {
match event {
Event::WindowEvent { event: WindowEvent::CloseRequested, .. } => elwt.exit(),
Event::AboutToWait => {
window.request_redraw();
},
Event::WindowEvent {
window_id, event: WindowEvent::RedrawRequested
} if window_id == window.id() => {
// 現在のウインドウサイズを取得
let (width, height) = {
let size = window.inner_size();
(size.width, size.height)
};
// surface を画面サイズにリサイズ
surface.resize(
core::num::NonZeroU32::new(width).unwrap(),
core::num::NonZeroU32::new(height).unwrap(),
).unwrap();
// 描画のためのピクセルバッファを生成
let mut pixmap = Pixmap::new(width, height).unwrap();
draw_block(&mut pixmap);
// 画面バッファに反映
let mut buffer = surface.buffer_mut().unwrap();
for index in 0..(width * height) as usize {
buffer[index] =
pixmap.data()[index * 4 + 2] as u32
| (pixmap.data()[index * 4 + 1] as u32) << 8
| (pixmap.data()[index * 4 + 0] as u32) << 16;
}
buffer.present().unwrap();
},
_ => ()
}
});
}
/// ピクセルバッファに正方形を書き込み
fn draw_block(pixmap: &mut Pixmap) {
let rect = Rect::from_xywh(190.0, 90.0, 20.0, 20.0).unwrap();
let path = PathBuilder::from_rect(rect);
let mut paint = Paint::default();
paint.set_color_rgba8(104, 102, 204, 255);
pixmap.fill_path(
&path,
&paint,
FillRule::EvenOdd,
Transform::identity(),
None,
);
}
このコードを実装すると、以下のようなウインドウが表示されます。
四角形は draw_block() 関数で描画しており、これを模倣することで、ゲームの描画ができそうです。
Titris のウインドウ表示
#ウインドウの描画について概略が分かったので、Titris のウインドウの描画に入ります。
main() 関数は以下のようになります。
use winit::event::{ Event, WindowEvent };
use winit::event_loop::{ ControlFlow, EventLoop };
use winit::window::WindowBuilder;
use winit::keyboard::{ Key::Named, NamedKey };
use tiny_skia::{ FillRule, Paint, PathBuilder, Pixmap, Rect, Transform };
fn main() {
let event_loop = EventLoop::new().unwrap();
event_loop.set_control_flow(ControlFlow::Poll);
let window = WindowBuilder::new()
.with_inner_size(winit::dpi::LogicalSize::new(BOARD_WIDTH * UNIT_SIZE, BOARD_HEIGHT * UNIT_SIZE))
.with_title("Titris")
.build(&event_loop).unwrap();
let window = std::rc::Rc::new(window);
let context = softbuffer::Context::new(window.clone()).unwrap();
let mut surface = softbuffer::Surface::new(&context, window.clone()).unwrap();
let mut game: Game = Game::new(); // <1> Game インスタンス生成
let _ = event_loop.run(move |event, elwt| {
match event {
Event::WindowEvent { event: WindowEvent::CloseRequested, .. } => elwt.exit(),
Event::WindowEvent {
event: WindowEvent::KeyboardInput {event, .. },
..
} if event.state.is_pressed() => {
// <2> キー入力により game 操作
match event.logical_key {
Named(NamedKey::ArrowRight) => game.key_pressed(Key::RIGHT),
Named(NamedKey::ArrowLeft) => game.key_pressed(Key::LEFT),
Named(NamedKey::ArrowDown) => game.key_pressed(Key::DOWN),
Named(NamedKey::ArrowUp) => game.key_pressed(Key::UP),
Named(NamedKey::Space) => game.key_pressed(Key::SP),
_ => game.key_pressed(Key::OTHER),
};
window.request_redraw();
},
Event::AboutToWait => {
// <3> ゲームの進行
if !game.stopped {
game.tick();
window.set_title(format!("Titris:{}", game.score).as_str());
window.request_redraw();
}
},
Event::WindowEvent {
window_id, event: WindowEvent::RedrawRequested
} if window_id == window.id() => {
let (width, height) = {
let size = window.inner_size();
(size.width, size.height)
};
surface.resize(
core::num::NonZeroU32::new(width).unwrap(),
core::num::NonZeroU32::new(height).unwrap(),
).unwrap();
let mut pixmap = Pixmap::new(width, height).unwrap();
// <4> ゲームの描画
game.draw(&mut pixmap);
let mut buffer = surface.buffer_mut().unwrap();
for index in 0..(width * height) as usize {
buffer[index] =
pixmap.data()[index * 4 + 2] as u32
| (pixmap.data()[index * 4 + 1] as u32) << 8
| (pixmap.data()[index * 4 + 0] as u32) << 16;
}
buffer.present().unwrap();
},
_ => ()
}
});
}
ざっと以下の点だけ見ておけば十分です。
- ゲームのインスタンスを生成し、
mutで可変とする - キーボード入力イベントに応じてゲームインスタンスを操作(ブロックの移動と回転、及び落下)
- ゲームの進行とスコアの更新
- ゲームの描画
テトロミノの色定義
#描画時には Tetromino を色分けするので、Tetromino に応じた色を返す関数を追加しておきましょう。
impl Tetromino {
fn color(&self) -> (u8, u8, u8) {
match self {
Tetromino::S => (204, 102, 102),
Tetromino::Z => (102, 204, 102),
Tetromino::I => (104, 102, 204),
Tetromino::T => (204, 204, 102),
Tetromino::O => (204, 102, 204),
Tetromino::J => (204, 204, 204),
Tetromino::L => (218, 170, 0),
_ => ( 0, 0, 0)
}
}
}
この定義は、既存の impl Tetromino { ... } の中に含めても良いですし、上記コードをそのままソース・ファイルに追記しても良いです。
color() メソッドでは、自身の種類に応じて、RGB値をタプルとして返します。
ゲームの描画
#最後に Game の描画処理の実装を追加します。
impl Game {
fn draw(&self, pixmap: &mut Pixmap) {
for y in 0..BOARD_HEIGHT {
for x in 0..BOARD_WIDTH {
Game::draw_square(pixmap, x, y, self.board[index_at(x, y)]);
}
}
for i in 0..4 {
let (x, y) = self.current.point(i);
Game::draw_square(pixmap, x, y, self.current.kind);
}
}
fn draw_square(pixmap: &mut Pixmap, x: i32, y: i32, kind: Tetromino) {
let x = x * UNIT_SIZE;
let y = (BOARD_HEIGHT - 1 - y) * UNIT_SIZE;
let rect = Rect::from_xywh(
(x + 1) as f32,
(y + 1) as f32,
(UNIT_SIZE - 2) as f32,
(UNIT_SIZE - 2) as f32,
).unwrap();
let path = PathBuilder::from_rect(rect);
let mut paint = Paint::default();
let (r ,g, b) = kind.color();
paint.set_color_rgba8(r, g, b, 255);
pixmap.fill_path(
&path,
&paint,
FillRule::EvenOdd,
Transform::identity(),
None,
);
}
}
draw() と draw_square() の2つで構成されています。
最初にある draw() メソッドから見ていきましょう。
fn draw(&self, pixmap: &mut Pixmap) {
for y in 0..BOARD_HEIGHT {
for x in 0..BOARD_WIDTH {
Game::draw_square(pixmap, x, y, self.board[index_at(x, y)]);
}
}
for i in 0..4 {
let (x, y) = self.current.point(i);
Game::draw_square(pixmap, x, y, self.current.kind);
}
}
引数は、 Pixmap を取る関数となっています。Pixmap は tiny_skia クレートにより提供され構造体で、2次元の RGBA ピクセル情報を持ちます。pixmap に書き込んだグラフィックスの内容が、画面バッファを介して実際のディスプレイに描画されます。
draw() メソッドの中身は2つの部分から構成されます。
最初の for ループにて、盤面のブロックを描画します。盤面の左上から右下に向かって、それぞれのマス目に対して draw_square() 関数を呼び出しています。draw_square() の呼び出しは、pixmap と、盤面の x, y 座標、マスに存在する単ブロックの種類を引数として渡しています。
続く for ループでは、現在の落下ブロックを描画します。ブロックを構成する4つの単ブロックに対して、draw_square() をpixmap 、ブロックの x, y 座標、ブロックの種類(Tetromino)を引数として渡しています。
この draw() メソッドは、main() 関数内の以下のようなイベントループから呼び出されます。
let _ = event_loop.run(move |event, elwt| {
match event {
// ...
Event::WindowEvent {
window_id, event: WindowEvent::RedrawRequested
} if window_id == window.id() => {
// ...
let mut pixmap = Pixmap::new(width, height).unwrap();
game.draw(&mut pixmap); // 描画の呼び出し
// ...
}
つまり、OSから再描画要求が行われた場合、イベントループに Event 型で通知が上がってくるため、これを パターンマッチで受け取り、game.draw(&mut pixmap); という形で呼び出されるわけです。
では、実際にブロックを描画する draw_square() の内容に移ります。
fn draw_square(pixmap: &mut Pixmap, x: i32, y: i32, kind: Tetromino) {
// ...
}
引数は Pixmap と x, y 座標、ブロックの種類 の4つの引数があります。ここで、x, y 座標は、盤面のマス目の位置であり、実際に表示する画面上のピクセル位置とは異なる点に注意してください。Tetromino は、ブロックを何色で描画するかの判断に使用します。
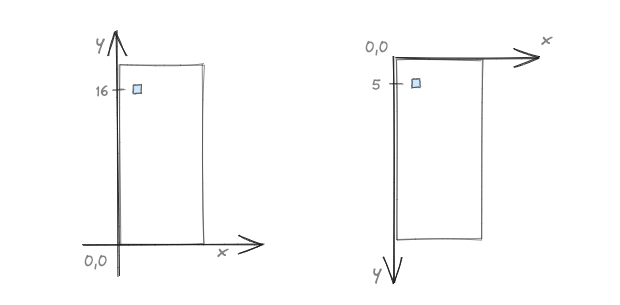
draw_square() の先頭で、座標変換を行っています。これまでの扱ってきた座標系は、左下を原点としてきましたが、ディスプレイの座標系は、左上が原点となります。そのため、盤面上部からブロックまでの距離が y 座標になります。
let x = x * UNIT_SIZE;
let y = (BOARD_HEIGHT - 1 - y) * UNIT_SIZE;
変換した x, y 座標に、1つのブロックの画面上のサイズ(ピクセル数)である UNIT_SIZE を乗算することで、Pixmap 上の位置に変換しています。
この座標位置に、Rect::from_xywh() により矩形を定義しています。
let rect = Rect::from_xywh(
(x + 1) as f32,
(y + 1) as f32,
(UNIT_SIZE - 2) as f32,
(UNIT_SIZE - 2) as f32,
).unwrap();
}
引数は、x, y 座標と幅と高さを指定します。ブロックの周りに1ピクセルの余白をつけるため、位置とサイズを調整しています(左右両側に1ピクセルの余白を設けるため、幅は2ピクセル小さくなります。上下についても同様です)。
この矩形をパスに変換し、色を指定して Pixmap に反映しているのが以下の処理です(これは tiny-skia クレートが提供する機能を使っているだけなので、このようにして使うんだ ぐらいの理解で十分です)。
let path = PathBuilder::from_rect(rect);
let mut paint = Paint::default();
let (r ,g, b) = kind.color();
paint.set_color_rgba8(r, g, b, 255);
pixmap.fill_path(
&path,
&paint,
FillRule::EvenOdd,
Transform::identity(),
None,
);
最後に、イベントループ上でのキー入力イベントと AboutToWait イベントについて再度見ておきましょう。
キー入力イベントは、そのキー内容に応じて、game インスタンスの key_pressed() メソッドを呼び出しています。
let _ = event_loop.run(move |event, elwt| {
match event {
// ...
Event::WindowEvent {
event: WindowEvent::KeyboardInput {event, .. },
..
} if event.state.is_pressed() => {
match event.logical_key {
Named(NamedKey::ArrowRight) => game.key_pressed(Key::RIGHT),
Named(NamedKey::ArrowLeft) => game.key_pressed(Key::LEFT),
Named(NamedKey::ArrowDown) => game.key_pressed(Key::DOWN),
Named(NamedKey::ArrowUp) => game.key_pressed(Key::UP),
Named(NamedKey::Space) => game.key_pressed(Key::SP),
_ => game.key_pressed(Key::OTHER),
};
window.request_redraw();
},
key_pressed() メソッドにより、ゲーム上の落下ブロックの位置が更新されます。キー入力後は、window.request_redraw(); により再描画を依頼しています。これにより再描画イベントがイベントループ上に登ってくるため、再描画のイベント処理が動くことで、画面描画が行われます。
イベントの処理が動作していない間は、AboutToWait イベントが定期的にイベントループ上に登ってくるため、これによりゲームの時間を進行させます。
let _ = event_loop.run(move |event, elwt| {
match event {
// ...
Event::AboutToWait => {
if !game.stopped {
game.tick();
window.set_title(format!("Titris:{}", game.score).as_str());
window.request_redraw();
}
},
game.tick() がその処理になります。この内容は既に見たもので、その後、スコアの更新と再描画要求を行っています。
Titris 完成
#さて、長かったですが、これにて全ての実装が完了です。
実行してみましょう。
cargo run
動きましたか?
左右キーで移動。上下キーで回転。スペースキーで最下部まで落下。その他のキーで1段落下となります。

はい。動いています!
まとめ
#かなり長い記事になってしまいましたが、いかがでしたでしょうか。
Titris を動かすことができたでしょうか。
作成した Titris にはリトライの機能がありません。ゲームオーバーになったらウインドウを閉じるしかありません。
Esc キーでリスタートを行う機能を加えることを、チャレンジ課題として残しておきました。
余裕のあるかたは取り組んでみてください。
Esc キーは Named(NamedKey::Escape) => のようにパターンマッチできます。
ゲーム盤面の初期化は self.board = [Tetromino::X; (BOARD_WIDTH * BOARD_HEIGHT) as usize]; のように盤面を Tetromino::X で満たすことで実現できます。
最後にソースコード全体を乗せておきます(main.rs ファイルにそのまま貼り付ければ動作するはずです)。
use winit::event::{ Event, WindowEvent };
use winit::event_loop::{ ControlFlow, EventLoop };
use winit::window::WindowBuilder;
use winit::keyboard::{ Key::Named, NamedKey };
use tiny_skia::{ FillRule, Paint, PathBuilder, Pixmap, Rect, Transform };
const UNIT_SIZE: i32 = 20;
const BOARD_WIDTH: i32 = 10;
const BOARD_HEIGHT: i32 = 22;
enum Key { LEFT, RIGHT, UP, DOWN, SP, OTHER, }
fn main() {
let event_loop = EventLoop::new().unwrap();
event_loop.set_control_flow(ControlFlow::Poll);
let window = WindowBuilder::new()
.with_inner_size(winit::dpi::LogicalSize::new(BOARD_WIDTH * UNIT_SIZE, BOARD_HEIGHT * UNIT_SIZE))
.with_title("Titris")
.build(&event_loop).unwrap();
let window = std::rc::Rc::new(window);
let context = softbuffer::Context::new(window.clone()).unwrap();
let mut surface = softbuffer::Surface::new(&context, window.clone()).unwrap();
let mut game: Game = Game::new();
let _ = event_loop.run(move |event, elwt| {
match event {
Event::WindowEvent { event: WindowEvent::CloseRequested, .. } => elwt.exit(),
Event::WindowEvent {
event: WindowEvent::KeyboardInput {event, .. },
..
} if event.state.is_pressed() => {
match event.logical_key {
Named(NamedKey::ArrowRight) => game.key_pressed(Key::RIGHT),
Named(NamedKey::ArrowLeft) => game.key_pressed(Key::LEFT),
Named(NamedKey::ArrowDown) => game.key_pressed(Key::DOWN),
Named(NamedKey::ArrowUp) => game.key_pressed(Key::UP),
Named(NamedKey::Space) => game.key_pressed(Key::SP),
_ => game.key_pressed(Key::OTHER),
};
window.request_redraw();
},
Event::AboutToWait => {
if !game.stopped {
game.tick();
window.set_title(format!("Titris:{}", game.score).as_str());
window.request_redraw();
}
},
Event::WindowEvent {
window_id, event: WindowEvent::RedrawRequested
} if window_id == window.id() => {
let (width, height) = {
let size = window.inner_size();
(size.width, size.height)
};
surface.resize(
core::num::NonZeroU32::new(width).unwrap(),
core::num::NonZeroU32::new(height).unwrap(),
).unwrap();
let mut pixmap = Pixmap::new(width, height).unwrap();
game.draw(&mut pixmap);
let mut buffer = surface.buffer_mut().unwrap();
for index in 0..(width * height) as usize {
buffer[index] =
pixmap.data()[index * 4 + 2] as u32
| (pixmap.data()[index * 4 + 1] as u32) << 8
| (pixmap.data()[index * 4 + 0] as u32) << 16;
}
buffer.present().unwrap();
},
_ => ()
}
});
}
#[derive(Copy, Clone, Debug, PartialEq)]
enum Tetromino { I, O, T, J, L, S, Z, X, }
impl Tetromino {
fn rand() -> Self {
match rand::random::<u32>() % 7 {
0 => Tetromino::I, 1 => Tetromino::O,
2 => Tetromino::T, 3 => Tetromino::J,
4 => Tetromino::L, 5 => Tetromino::S,
6 => Tetromino::Z, _ => Tetromino::X,
}
}
fn shape(&self) -> [[i32; 2]; 4] {
match self {
Tetromino::I => [[ 0, -1], [0, 0], [ 0, 1], [ 0, 2]],
Tetromino::O => [[ 0, 0], [1, 0], [ 0, 1], [ 1, 1]],
Tetromino::T => [[-1, 0], [0, 0], [ 1, 0], [ 0, -1]],
Tetromino::J => [[-1, -1], [0, -1], [ 0, 0], [ 0, 1]],
Tetromino::L => [[ 1, -1], [0, -1], [ 0, 0], [ 0, 1]],
Tetromino::S => [[ 0, -1], [0, 0], [-1, 0], [-1, 1]],
Tetromino::Z => [[ 0, -1], [0, 0], [ 1, 0], [ 1, 1]],
Tetromino::X => [[0; 2]; 4],
}
}
fn color(&self) -> (u8, u8, u8) {
match self {
Tetromino::S => (204, 102, 102),
Tetromino::Z => (102, 204, 102),
Tetromino::I => (104, 102, 204),
Tetromino::T => (204, 204, 102),
Tetromino::O => (204, 102, 204),
Tetromino::J => (204, 204, 204),
Tetromino::L => (218, 170, 0),
_ => ( 0, 0, 0)
}
}
}
#[derive(Copy, Clone, Debug)]
struct Block {
kind: Tetromino,
points: [[i32; 2]; 4],
x: i32, y: i32,
}
impl Block {
fn new(x: i32, y: i32) -> Self {
let kind = Tetromino::rand();
Block {
kind,
points: kind.shape(),
x,
y: y - kind.shape().iter().max_by_key(|p| p[1]).unwrap()[1],
}
}
fn empty() -> Self {
let kind = Tetromino::X;
Block { kind, points: kind.shape(), x: 0, y: 0 }
}
fn is_empty(&self) -> bool { self.kind == Tetromino::X }
fn point(&self, i: usize) -> (i32, i32) {
(self.x + self.points[i][0], self.y + self.points[i][1])
}
fn left(&self) -> Block { Block { x: self.x - 1, ..*self } }
fn right(&self) -> Block { Block { x: self.x + 1, ..*self } }
fn down(&self) -> Block { Block { y: self.y - 1, ..*self } }
fn rotate_right(&self) -> Block { self.rotate(true) }
fn rotate_left(&self) -> Block { self.rotate(false) }
fn rotate(&self, clockwise: bool) -> Block {
let mut points: [[i32; 2]; 4] = [[0; 2]; 4];
for i in 0..4 {
points[i] = if clockwise {
[self.points[i][1], -self.points[i][0]]
} else {
[-self.points[i][1], self.points[i][0]]
};
}
Block { points, ..*self }
}
}
fn index_at(x: i32, y: i32) -> usize {
(y * BOARD_WIDTH + x) as usize
}
struct Game {
board: [Tetromino; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block,
stopped: bool,
time: std::time::SystemTime,
score: u32,
}
impl Game {
fn new() -> Self {
Game {
board: [Tetromino::X; (BOARD_WIDTH * BOARD_HEIGHT) as usize],
current: Block::empty(),
stopped: false,
time: std::time::SystemTime::now(),
score: 0,
}
}
fn tick(&mut self) {
if self.current.is_empty() {
self.put_block();
} else if self.time.elapsed().unwrap() >
std::time::Duration::from_millis((1000 - self.score) as u64) {
self.down();
self.time = std::time::SystemTime::now();
}
}
fn put_block(&mut self) {
self.stopped = !self.try_move(Block::new(BOARD_WIDTH / 2, BOARD_HEIGHT - 1));
}
fn try_move(&mut self, block: Block) -> bool {
for i in 0..4 {
let (x, y) = block.point(i);
if x < 0 || x >= BOARD_WIDTH || y < 0 || y >= BOARD_HEIGHT {
return false;
}
if self.board[index_at(x, y)] != Tetromino::X {
return false;
}
}
self.current = block;
true
}
fn down(&mut self) {
if !self.try_move(self.current.down()) {
self.block_dropped();
}
}
fn drop_down(&mut self) {
while self.current.y > 0 {
if !self.try_move(self.current.down()) {
break;
}
}
self.block_dropped();
}
fn block_dropped(&mut self) {
for i in 0..4 {
let (x, y) = self.current.point(i);
self.board[index_at(x, y)] = self.current.kind;
}
self.remove_complete_lines();
if self.current.is_empty() {
self.put_block();
}
}
fn key_pressed(&mut self, key: Key) {
if self.stopped || self.current.is_empty() {
return;
}
match key {
Key::LEFT => { self.try_move(self.current.left()); },
Key::RIGHT => { self.try_move(self.current.right()); },
Key::UP => { self.try_move(self.current.rotate_right()); },
Key::DOWN => { self.try_move(self.current.rotate_left()); },
Key::OTHER => { self.down(); },
Key::SP => { self.drop_down(); },
};
}
fn remove_complete_lines(&mut self) {
let mut line_count = 0;
for y in (0..BOARD_HEIGHT).rev() {
let mut complete = true;
for x in 0.. BOARD_WIDTH {
if self.board[index_at(x, y)] == Tetromino::X {
// traverse the rows and if there is a blank, it cannot be completed
complete = false;
break
}
}
if complete {
line_count += 1;
// drop the line above the completed line
for dy in y..BOARD_HEIGHT - 1 {
for x in 0..BOARD_WIDTH {
// copy from the above line
self.board[index_at(x, dy)] = self.board[index_at(x, dy + 1)];
}
}
}
}
self.score += line_count * line_count;
self.current = Block::empty();
}
fn draw(&self, pixmap: &mut Pixmap) {
for y in 0..BOARD_HEIGHT {
for x in 0..BOARD_WIDTH {
Game::draw_square(pixmap, x, y, self.board[index_at(x, y)]);
}
}
for i in 0..4 {
let (x, y) = self.current.point(i);
Game::draw_square(pixmap, x, y, self.current.kind);
}
}
fn draw_square(pixmap: &mut Pixmap, x: i32, y: i32, kind: Tetromino) {
let x = x * UNIT_SIZE;
let y = (BOARD_HEIGHT - 1 - y) * UNIT_SIZE;
let rect = Rect::from_xywh(
(x + 1) as f32,
(y + 1) as f32,
(UNIT_SIZE - 2) as f32,
(UNIT_SIZE - 2) as f32,
).unwrap();
let path = PathBuilder::from_rect(rect);
let mut paint = Paint::default();
let (r ,g, b) = kind.color();
paint.set_color_rgba8(r, g, b, 255);
pixmap.fill_path(
&path,
&paint,
FillRule::EvenOdd,
Transform::identity(),
None,
);
}
}